Formelzusammenfassung:

Formel Radialbeschleunigung:

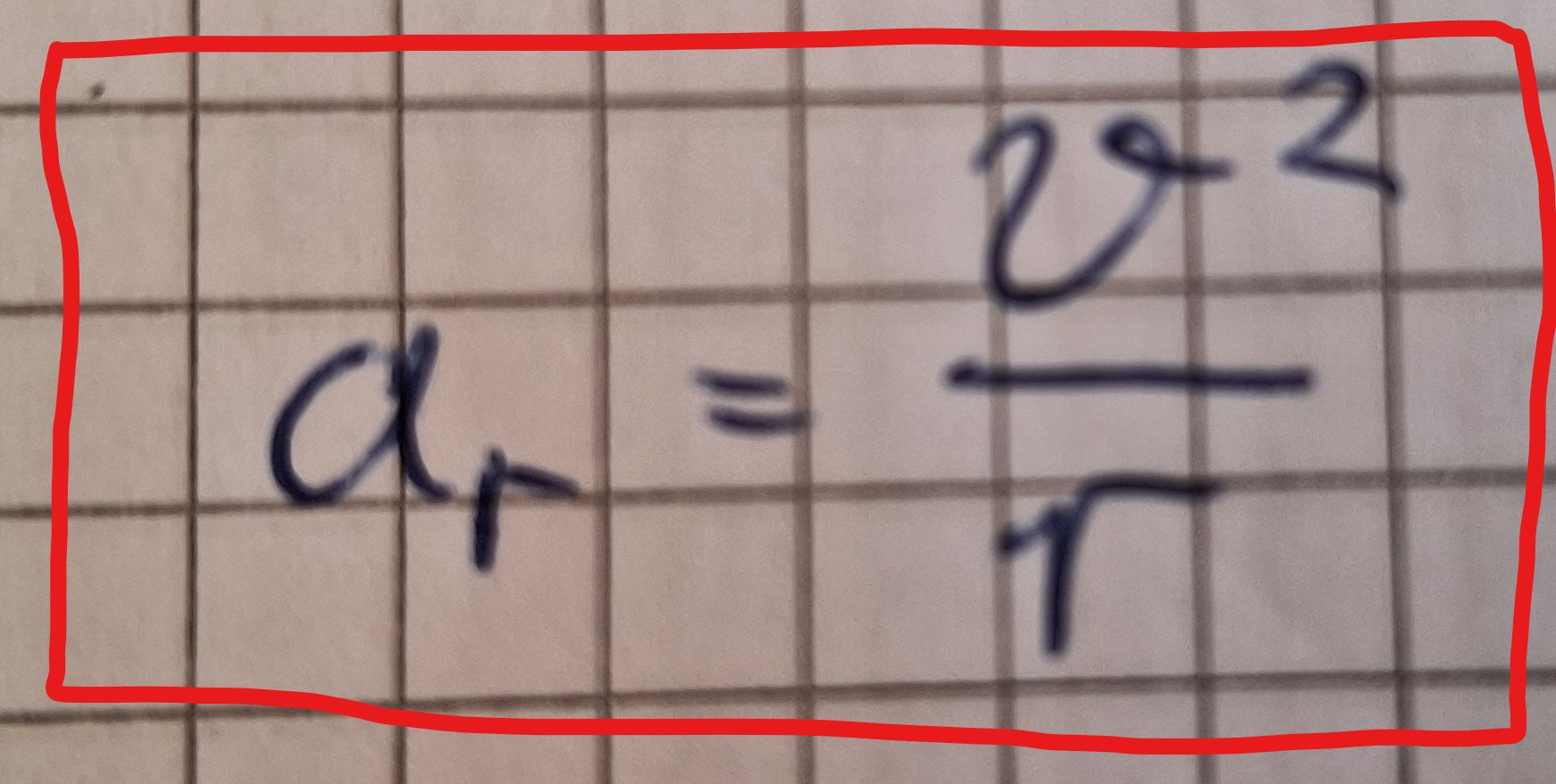
Gleichförmige Kreisbewegung , Radialbeschleunigung, krummlinige Bewegung.

Hier erkläre ich die Gleichförmige Kreisbewegung mit Herleitung.

Was ist eine geradlinige Bewegung: Die Traektorie der Bewegung ist eine gerade Linie.

Was ist eine krummlinige Bewegung: Die Traektorie der Bewegung ist krumm.

Zum Beispiel.

Wenn ein Körper von oben losgelassen wird, fällt es geradlinig nach unten.

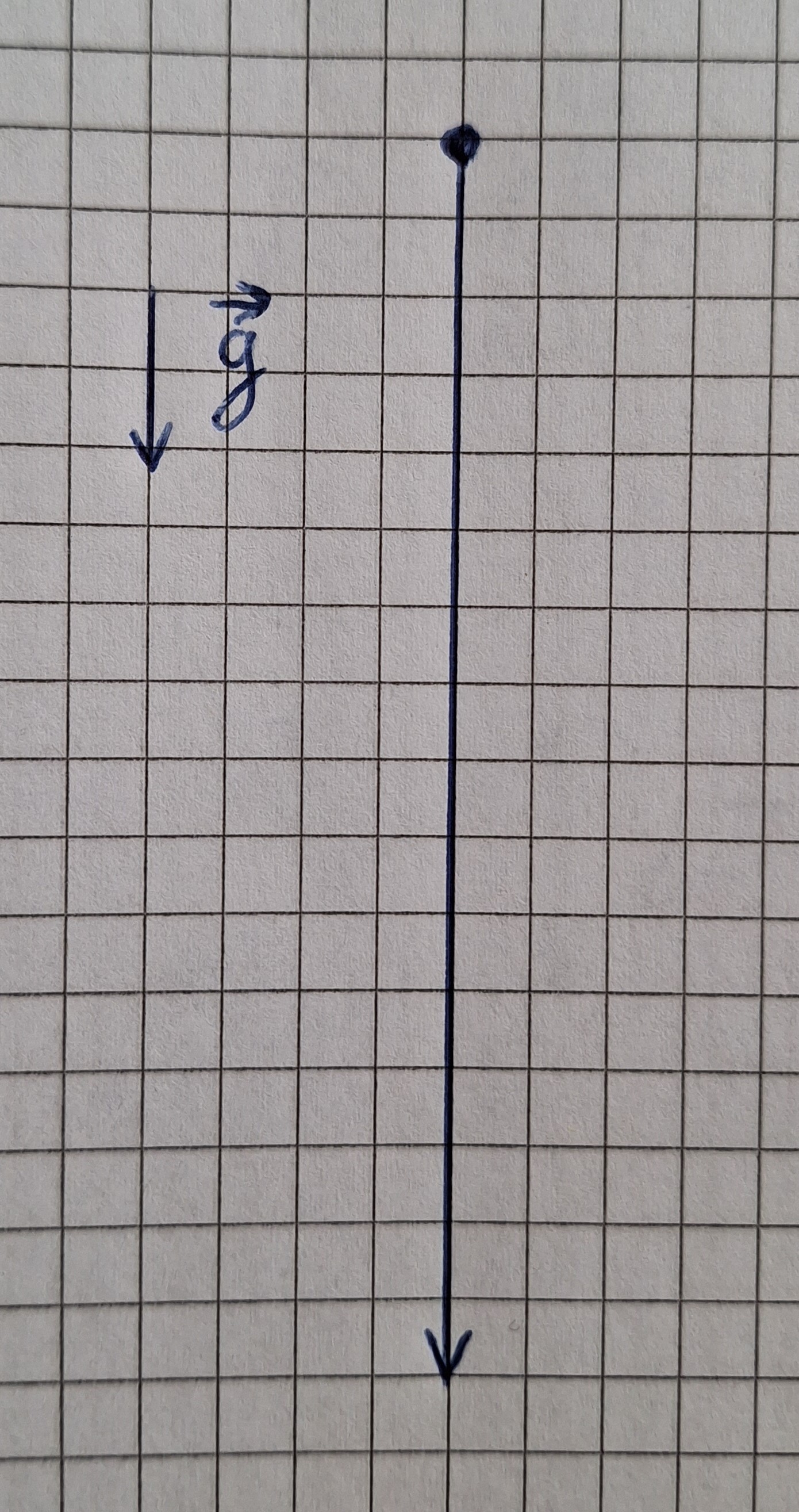
Wenn ein Körper in die Weite geworfen wird, fiegt es Krummlinig.

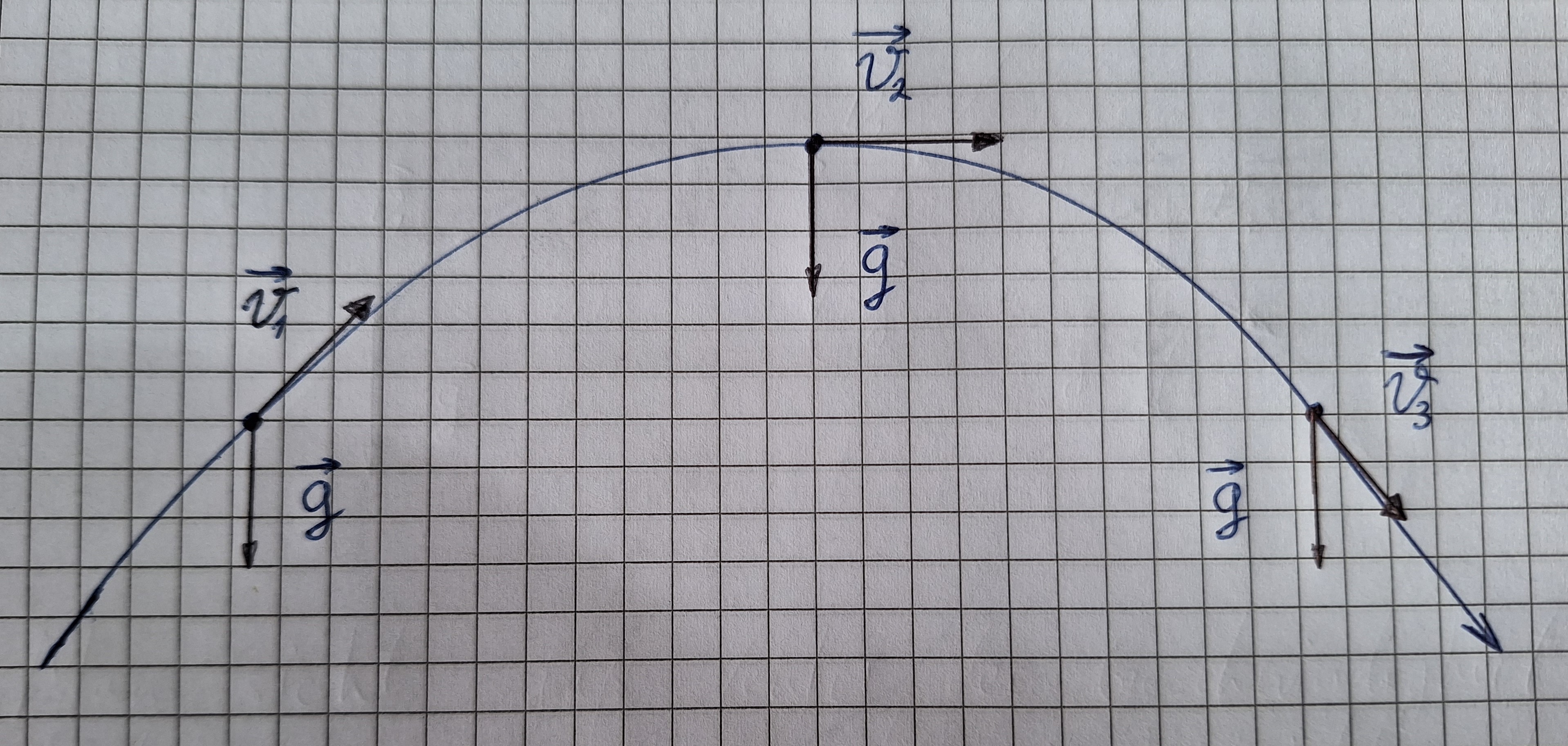
Man sieht, daß der Vektor der Geschwindigkeit v und der Vektor der Fallbeschleunigung g , nicht auf einer Geraden liegen.

Bei einer Krummlinigen Bewegung , liegt der Vektor der Geschwindigkeit und der Vektor der Beschleunigung nicht auf einer Geraden.

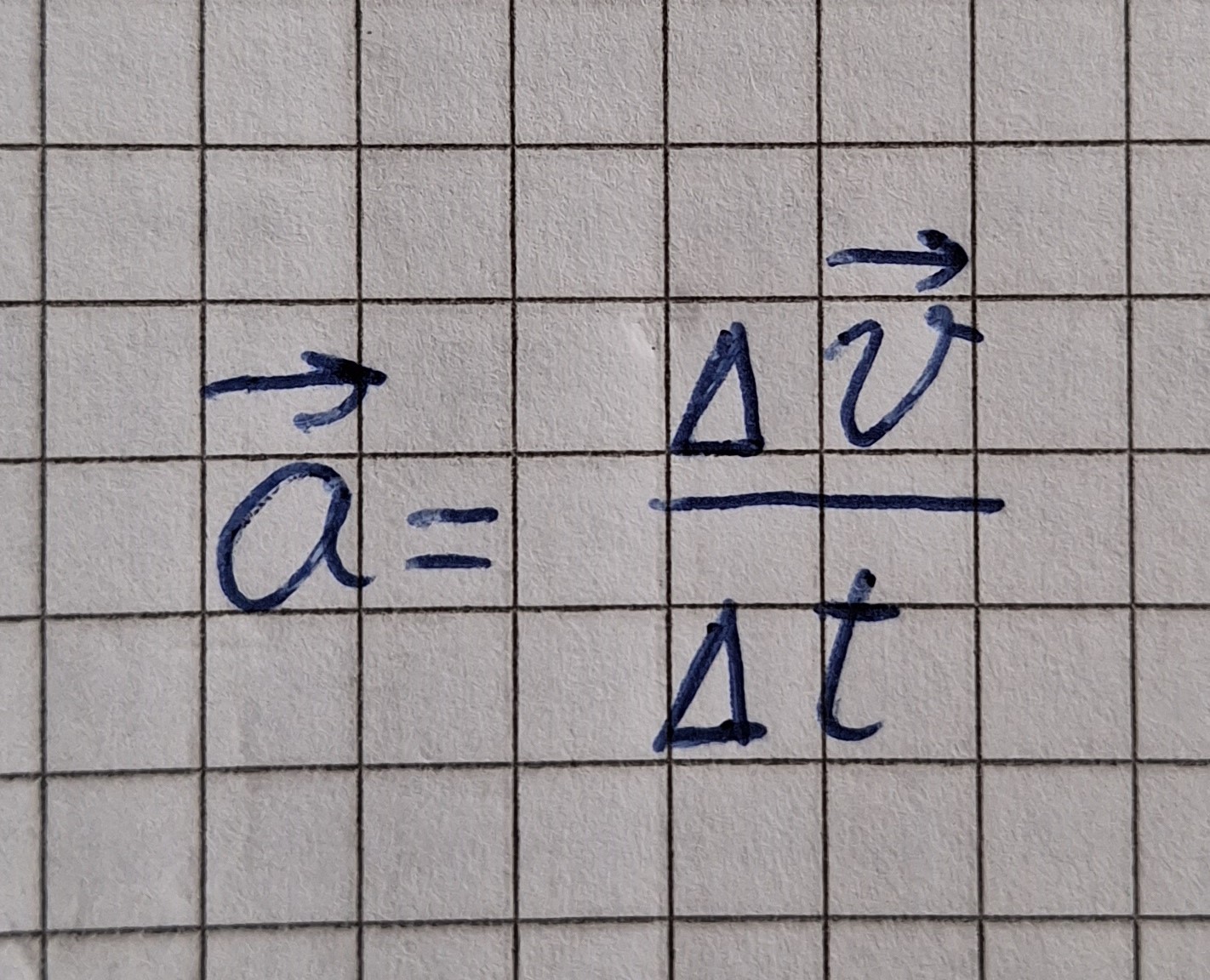
An der Formel sieht man. Der Vektor der änderung der Geschwindigkeit hat die gleiche Richtung wie der Vektor der Beschleunigung.

Kann eine krummlinige Bewegung ohne Beschleunigung sein?
Nein. Weil es bei einer krummlinigen Bewegung eine Änderung des Vektors der Geschwindigkeit gibt, und nach der Formel oben muß es auch eine Beschleunigung geben.(Die Richtung des Vektors ändert sich.)

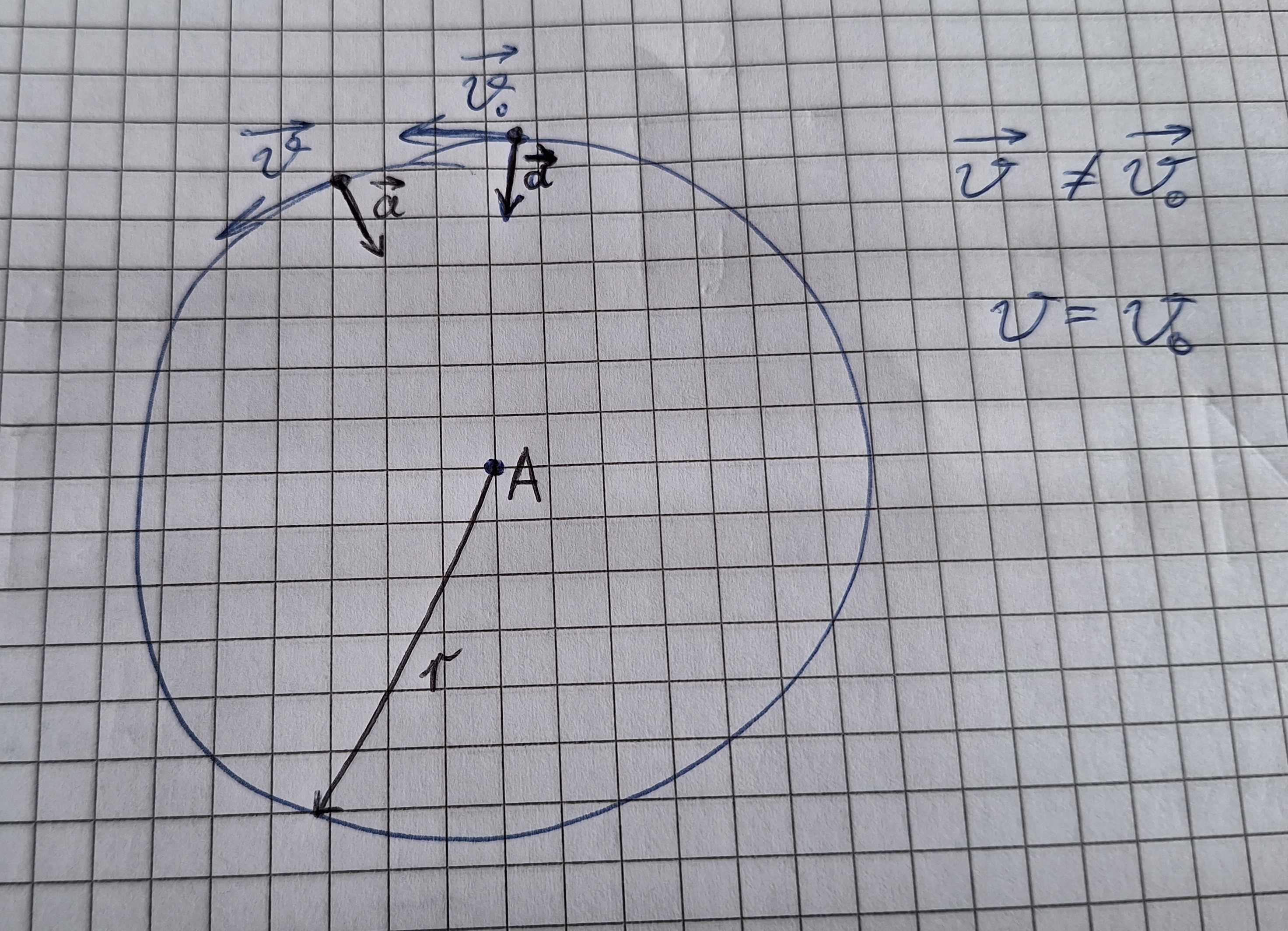
Eine gleichförmige Kreisbewegung.

Bei einer gleichförmigen Kreisbewegung ist der Betrag der Geschwindigkeit konstant. Und die Geschwindigkeit wird auch Bahngeschwindigkeit genannt.

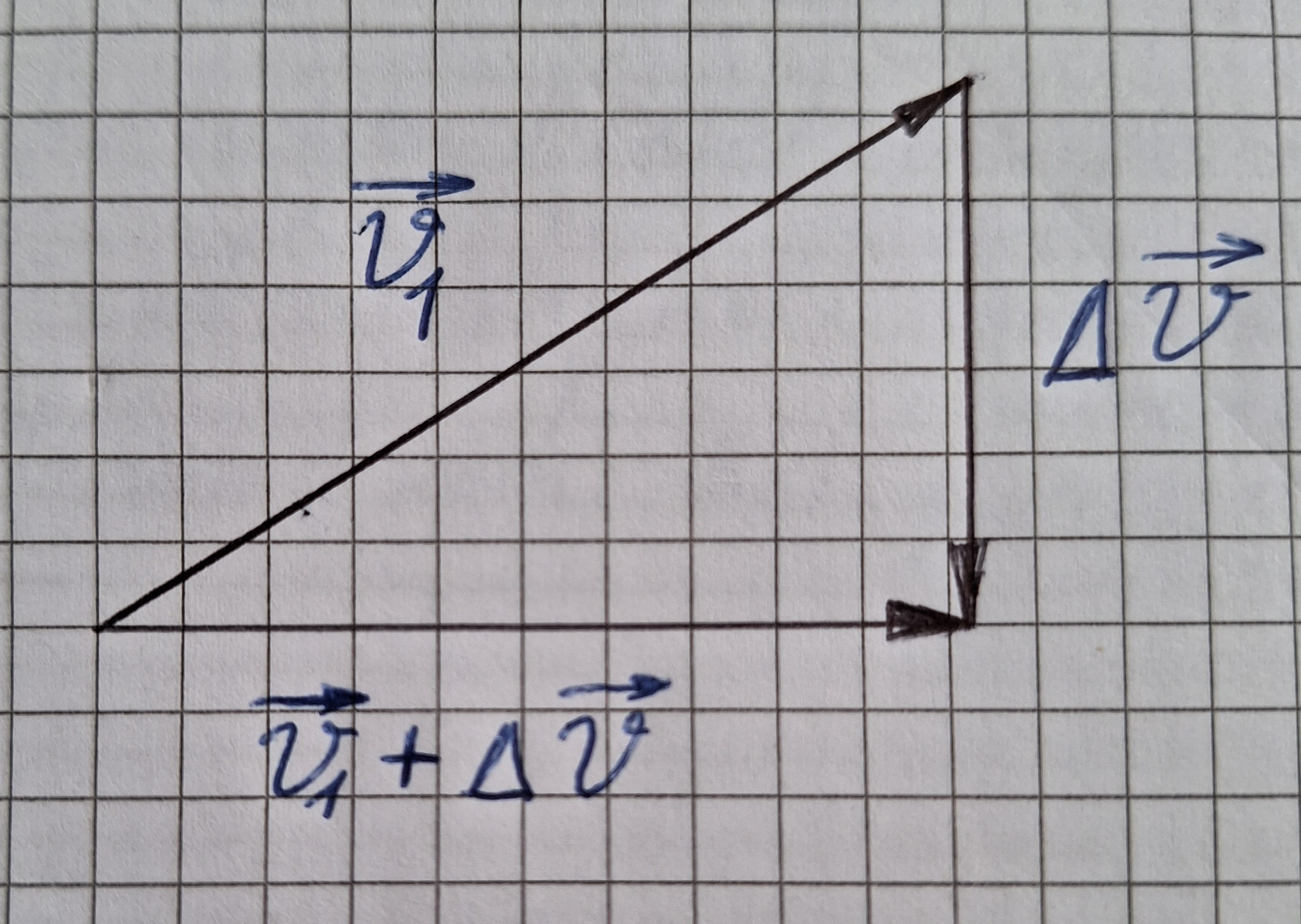
Die Vektoren von den Geschwindigkeiten v und v₀ sind verschieden , aber die Beträge sind gleich.

Wohin zeigt der Vektor der Beschleunigung a.

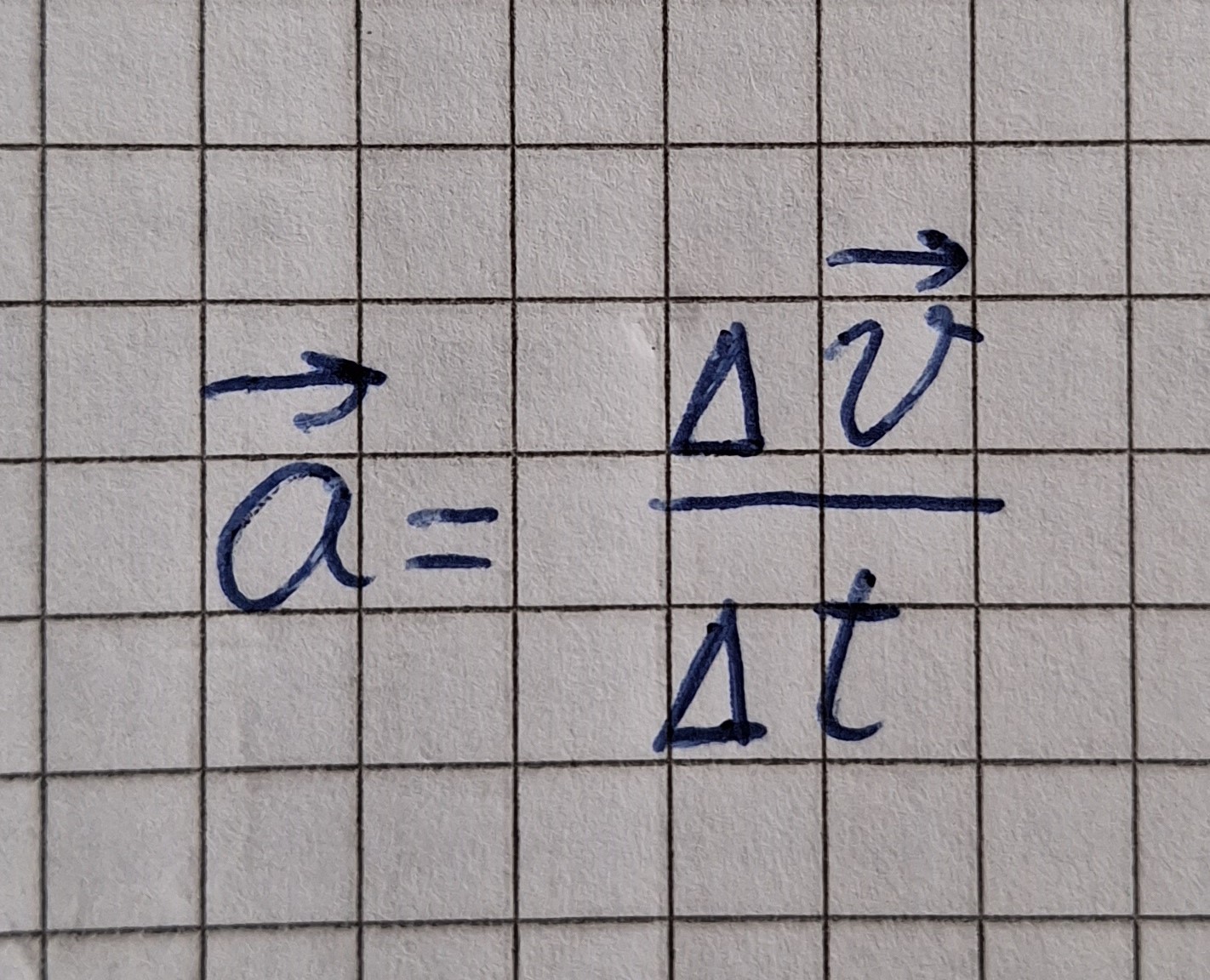
An der Formel sieht man, Vektor Δv und Vektor a haben die gleiche Richtung .

Zeichnen wir den Vektor Δv in der Zeichnung der Kreisbahn ein.

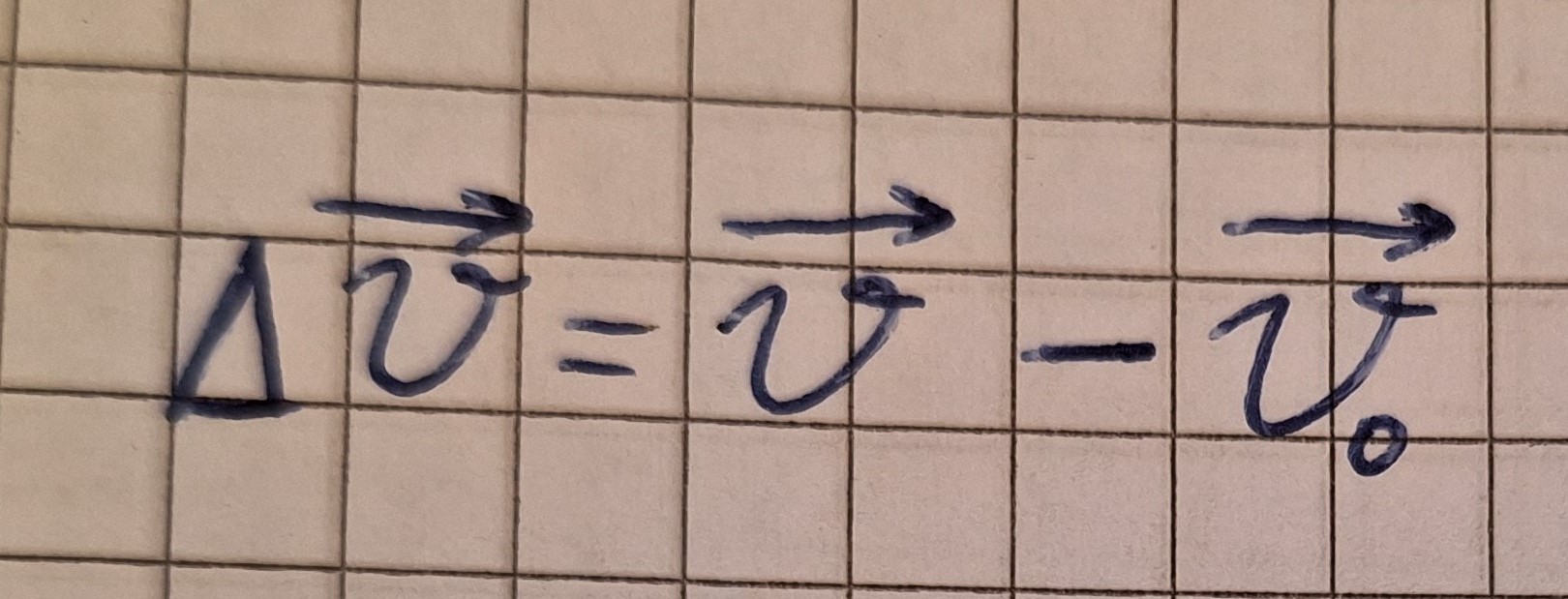
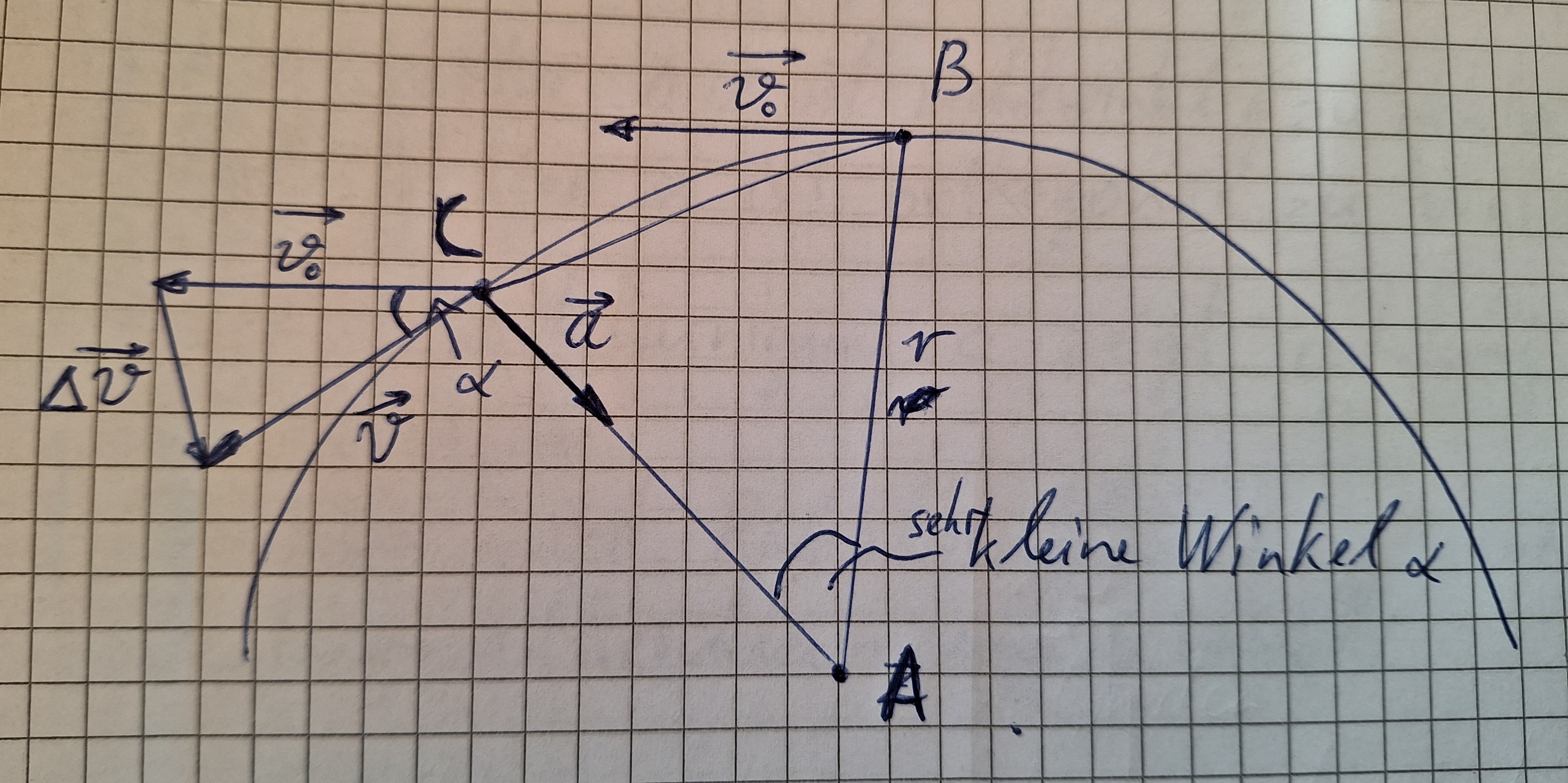
Der Vektor v₀ ist eine Tangente deswegen rechtwinklig zur Geraden BA.
Der Vektor v ist Rechtwinklig zur Geraden CA. A ist der Mittelpunkt der Kreisbahn.

Deshalb haben die beiden Dreiecke den gleichen Winkel α.

Da v=v₀ ist das Dreieck gleichschenklig, und die Basiswinkel sind gleich.
Die Summe der Winkel beim Dreieck ist 180°. Wenn α sehr klein ist , sind dann die Basiswinkel je fast 90°.

Also ist der Vektor Δv rechtwinklig zu Vektor v und v₀.

Wenn Δt gegen Null geht dann geht Winkel α gegen Null, dann ist der Vektor Δv rechtwinklig zu Vektor v.
daraus volgt Vektor a (Beschleunigung) ist orthogonal zu Vektor v.

Also Vektor a zeigt zum Zentrum vom Kreis.

Dise Beschleunigung a wird auch Radialbeschleunigung oder Zentripetalbeschleunigung genannt.

Betrag der Radialbeschleunigung (Zentripetalbeschleunigung). Berechnung und Herleitung.

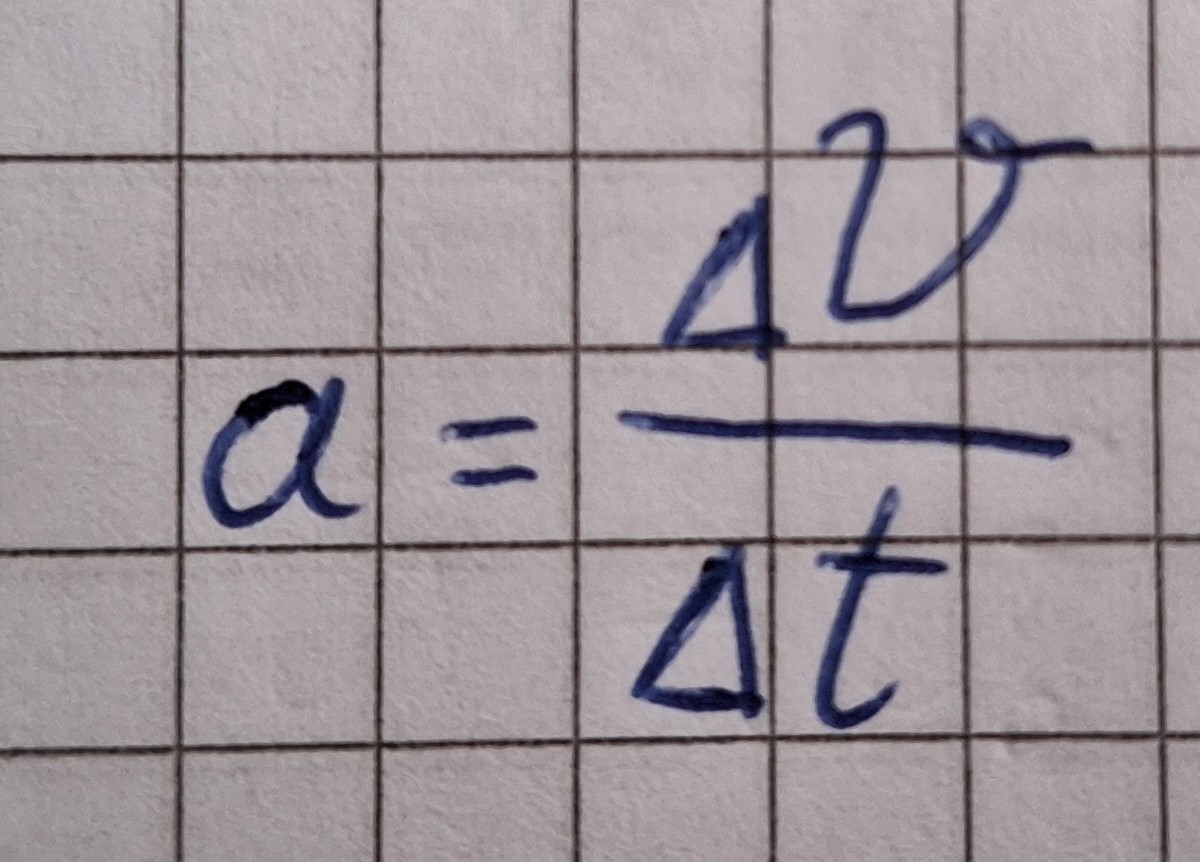
Formel vom Betrag der Beschleunigung.

In der Zeichnung oben sieht man, das die zwei Dreiecke ähnlich zu einander sind.
Daraus volgt:

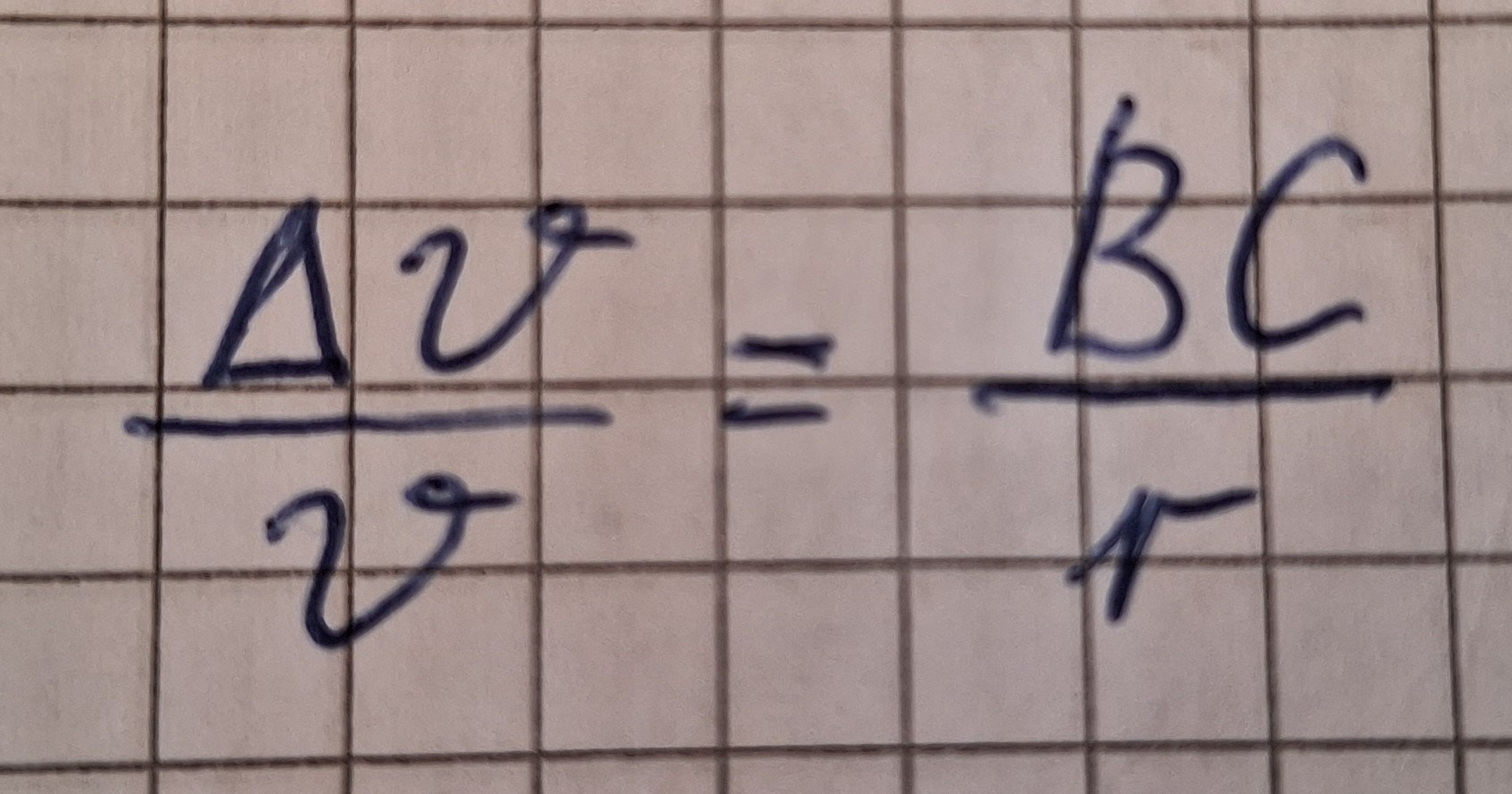
Bei Δt gegen Null wird die Strecke BC fast gleich dem Kreisbogen BC.

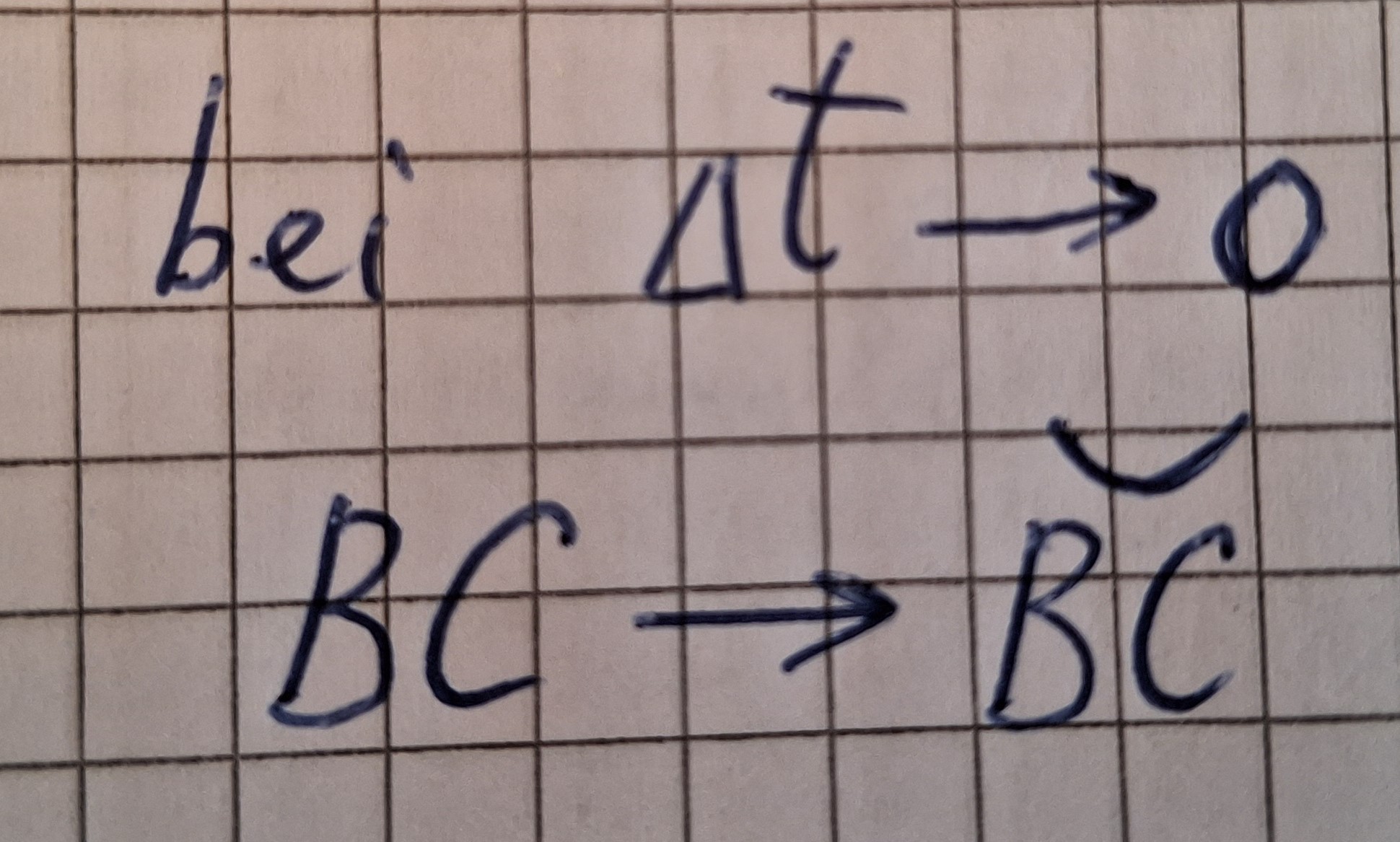
Deshalb:

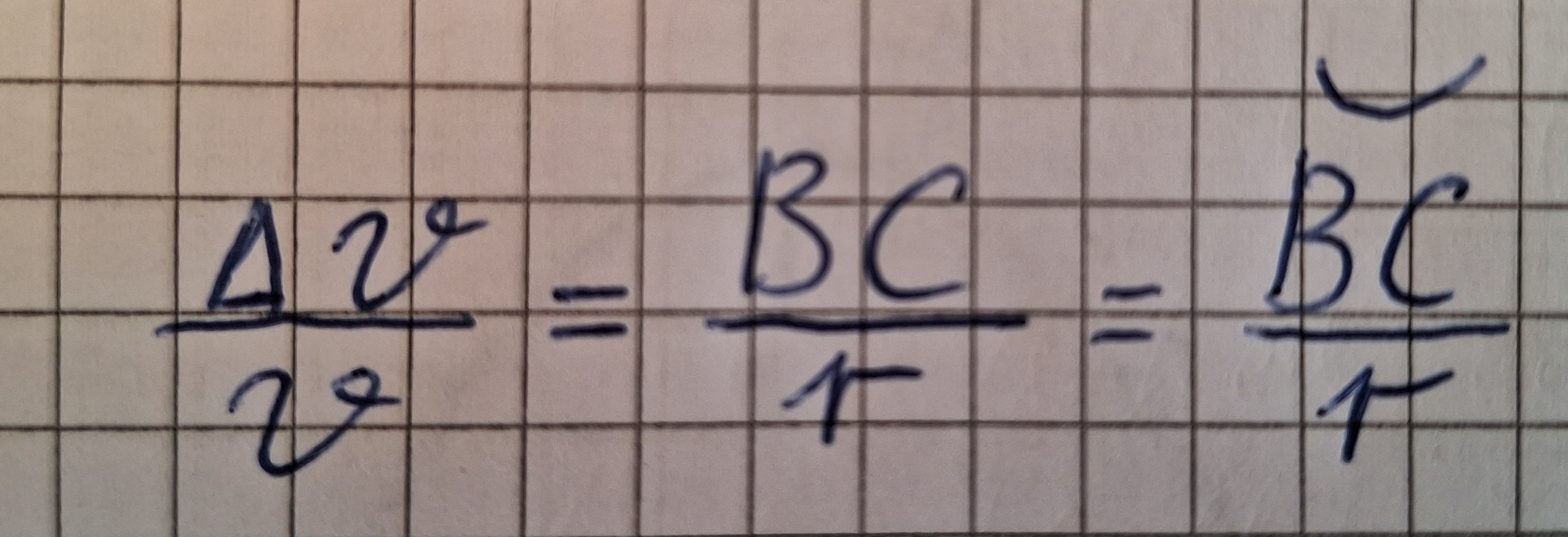
Da Geschwindigkeit (Tangential) mal Zeit geich länge von Kreisbogen ist.

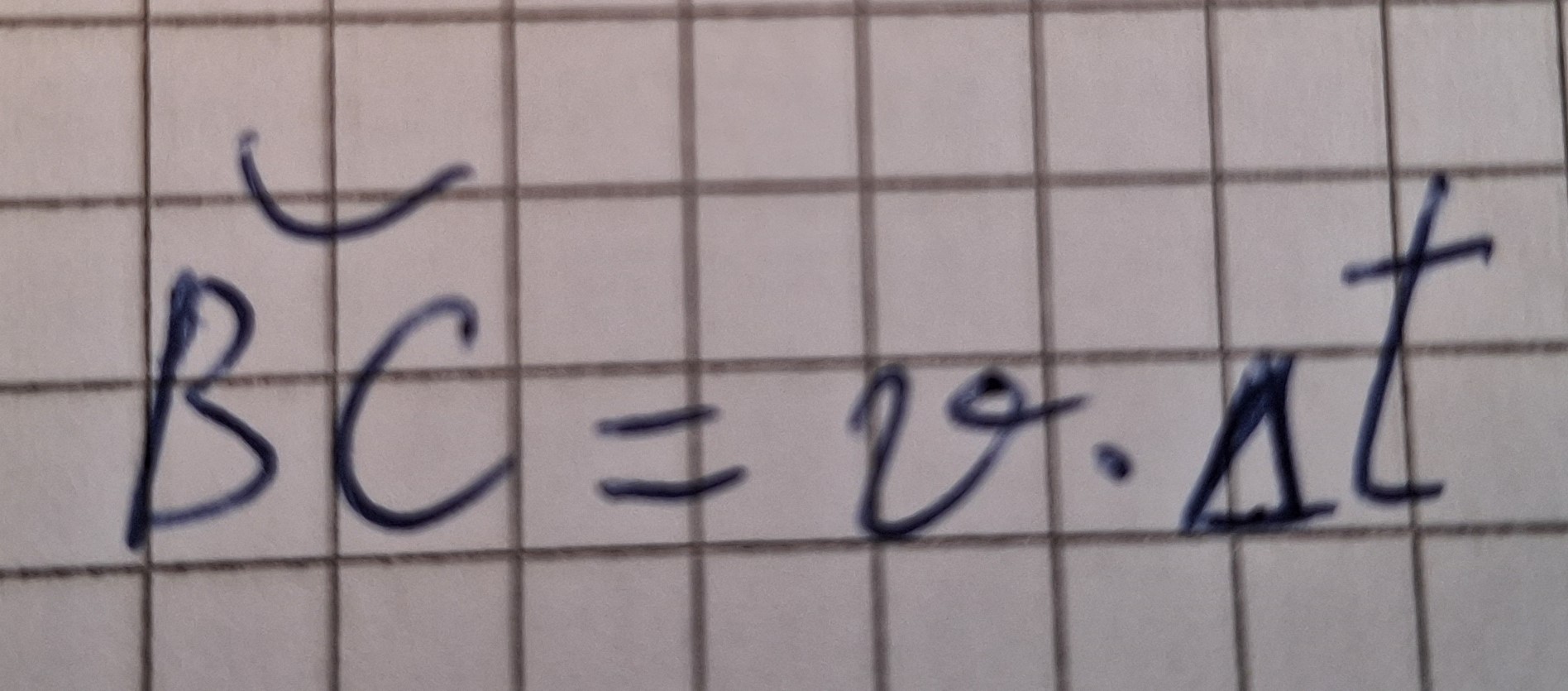
Dann das in die Formel einsetzen.

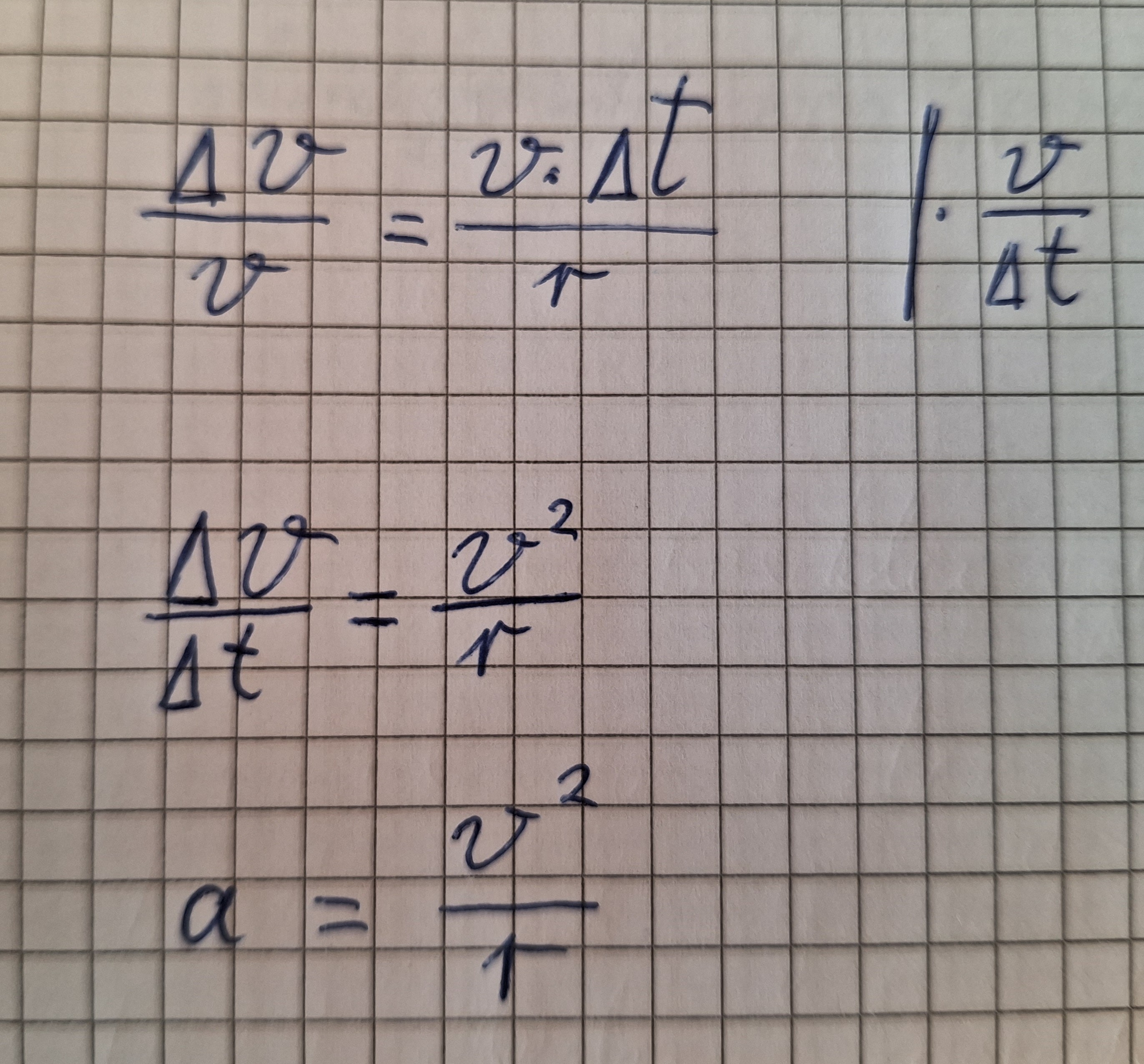
Zusammengefasst:

Formel Radialbeschleunigung:

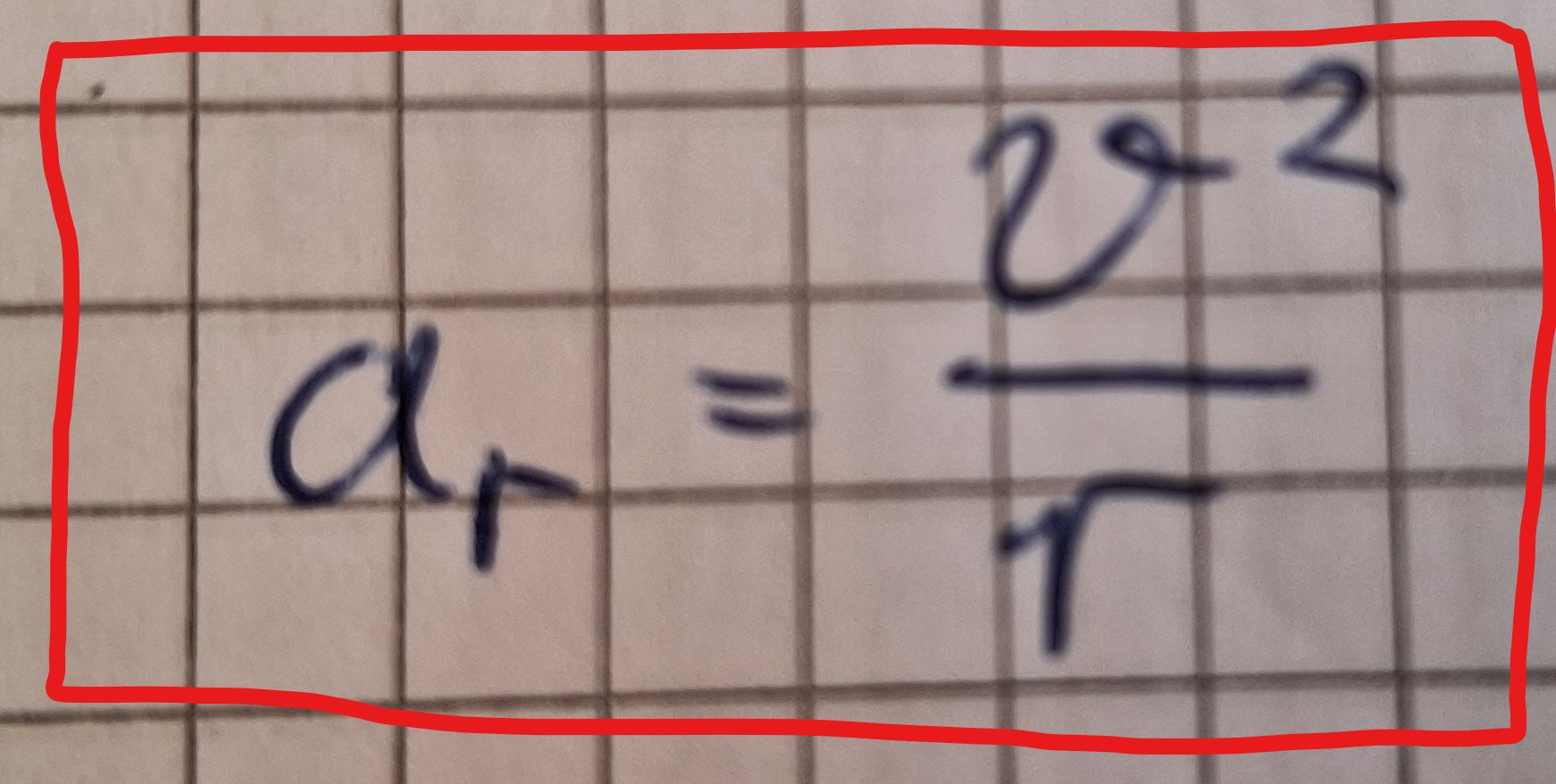
Vektor der Radialbeschleunigung a_r zeigt zum Zentrum des Kreises.

Gleichförmige Krummlinige Bewegung.

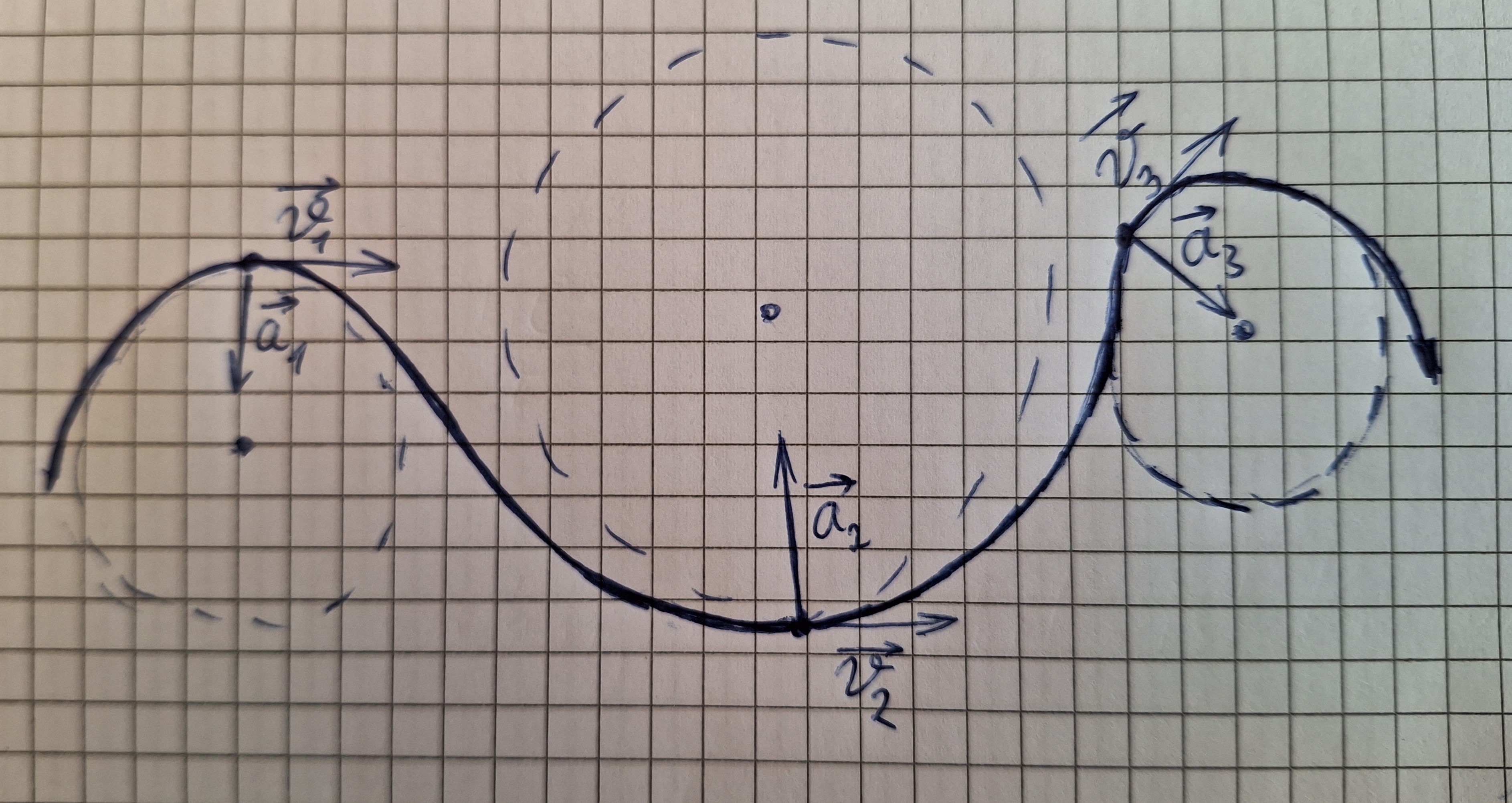
Mann kann eine gleichförmige krummlinige Bewegung in gleichförmige Kreisbewegungen zerlegen. Wie im Bild.

Beispiel zu gleichförmige Kreisbewegung .

Ein Sattelit der um die Erde kreist macht auch eine kreisförmige Bewegung. Durch die Erdanziehung (Fallbeschleunigung) wird er in der Kreisbahn gehalten.
An der Formel sieht man, das der Sattelit in seiner Höhe (Entfernung von Mittelpunkt der Erde) eine bestimmte Geschwindigkeit braucht.
Bei größerer Geschwindigkeit fliegt er höher und bei kleinerer Geschwindigkeit niedriger.

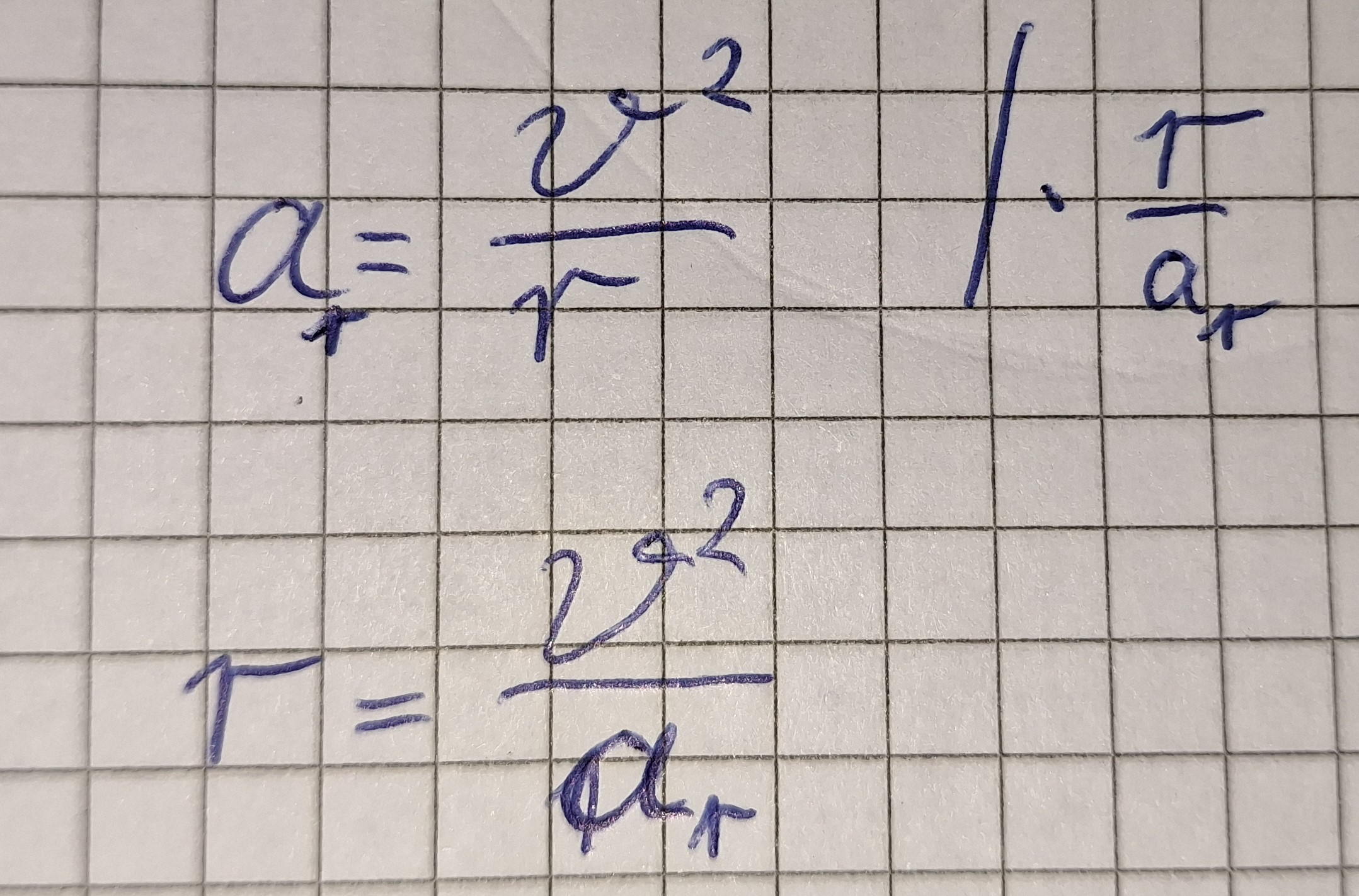
r ist proportional zu v² , wenn Geschwindigkeit 2 mal sich Vergrößert wird r 4 mal so groß.