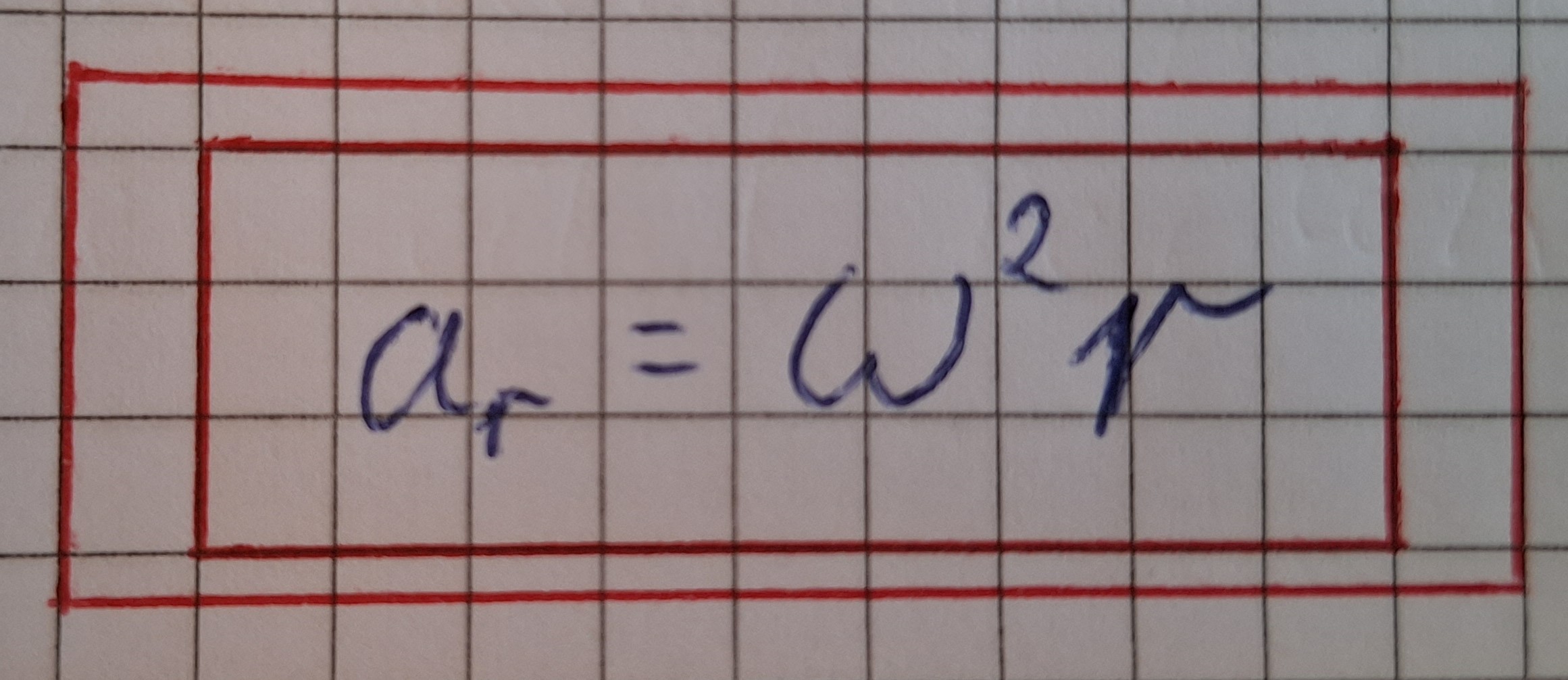Formel Zuammenfassung:
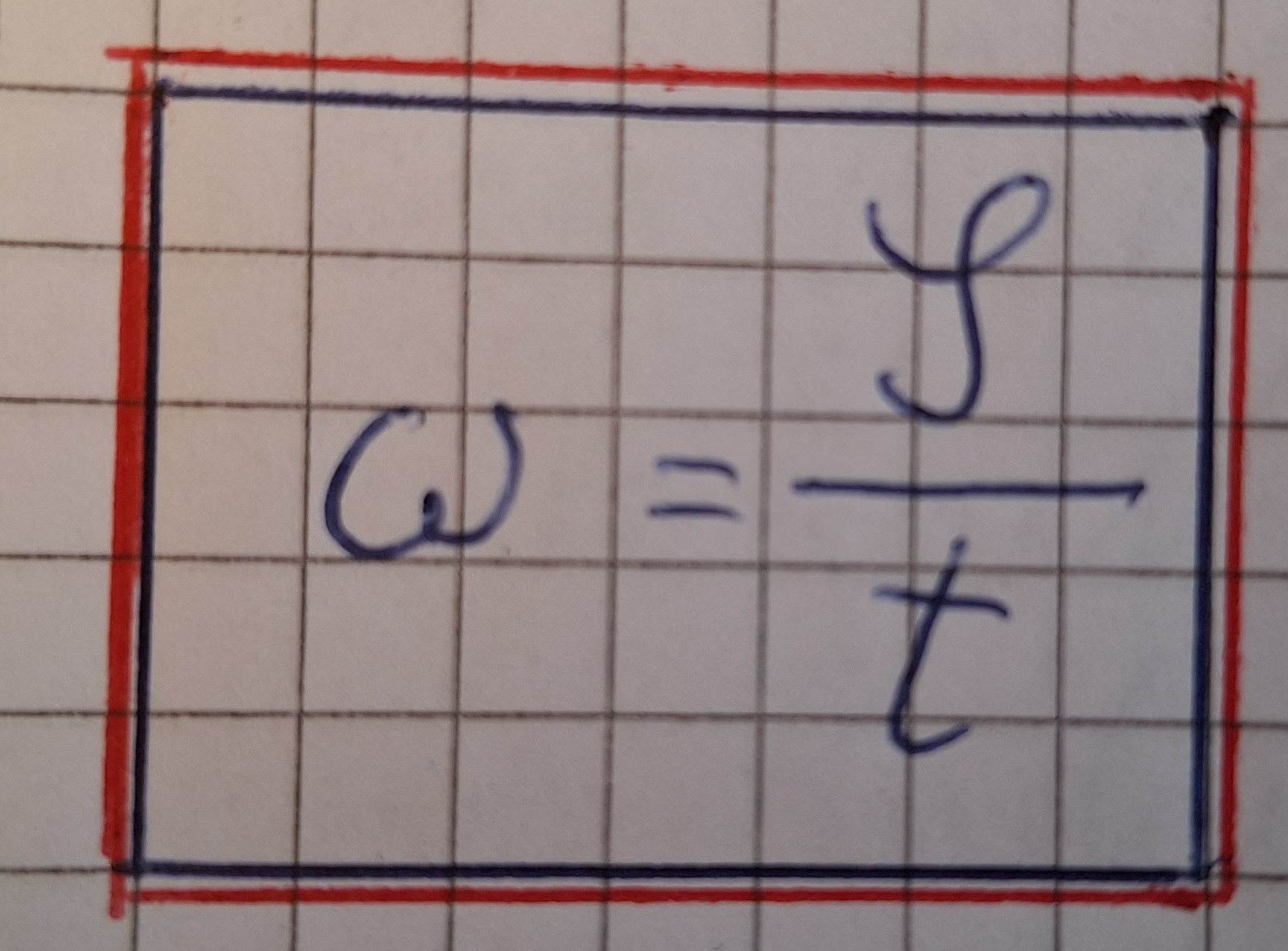
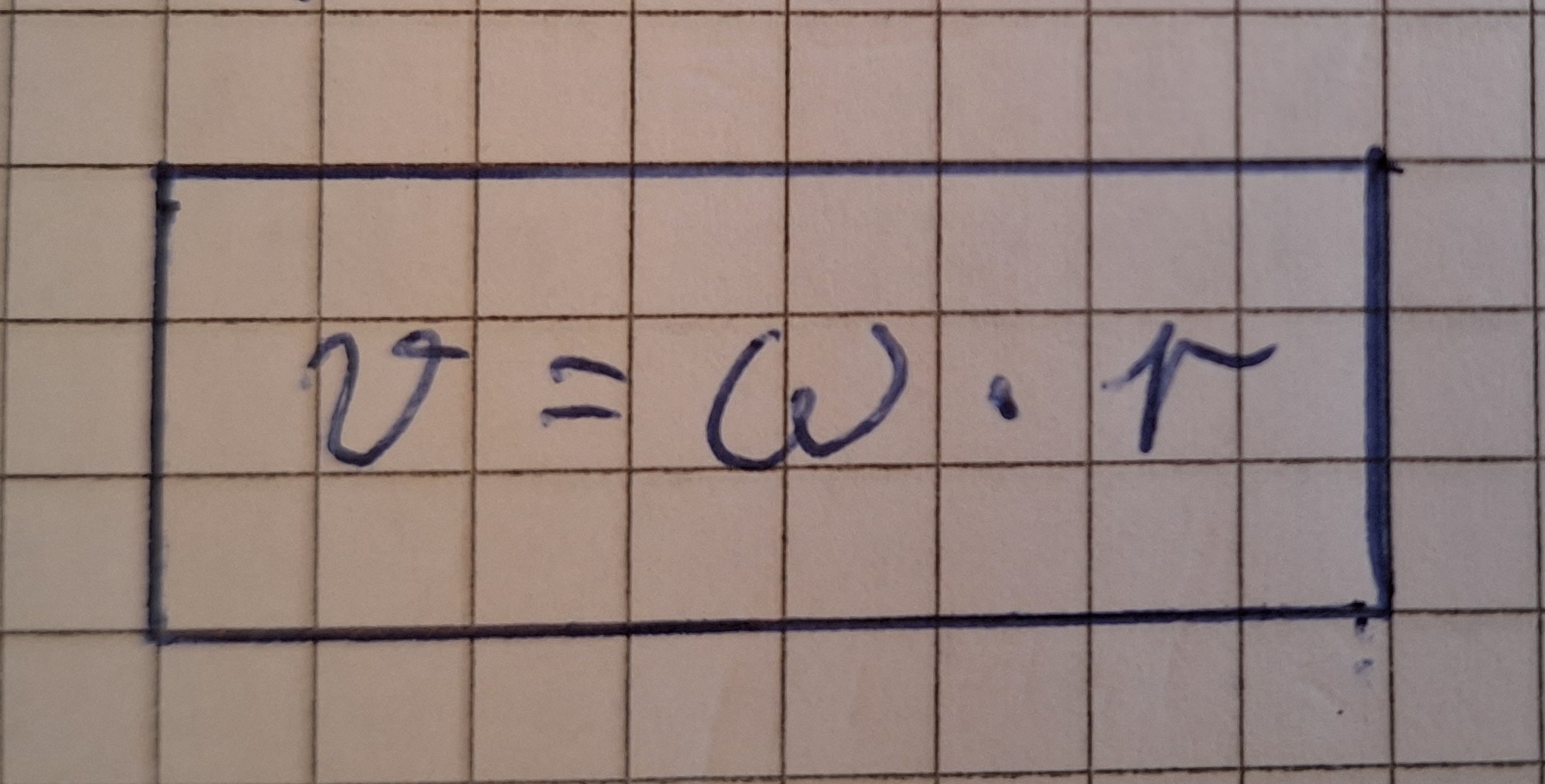
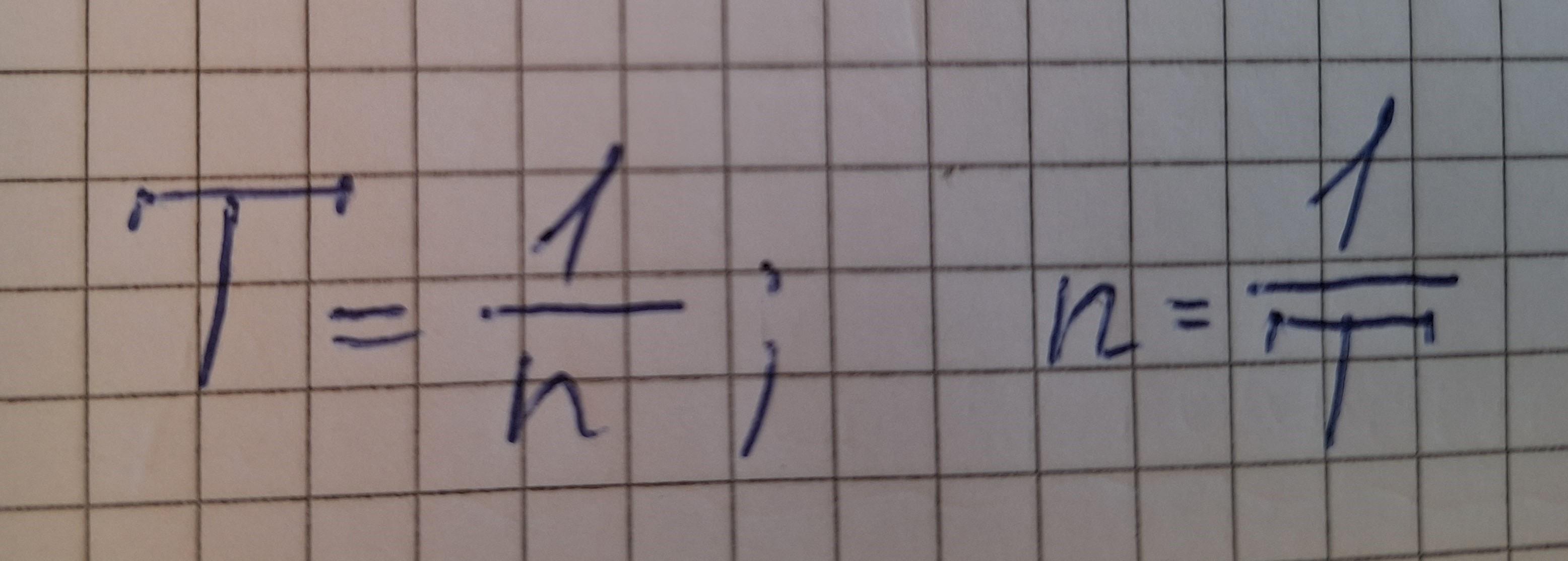
Geschwindigkeit und Winkelgeschwindigkeit
Frequenz und Periode der Drehbewegung
Drehbewegung von starren Körpern
Drehende starre Körper
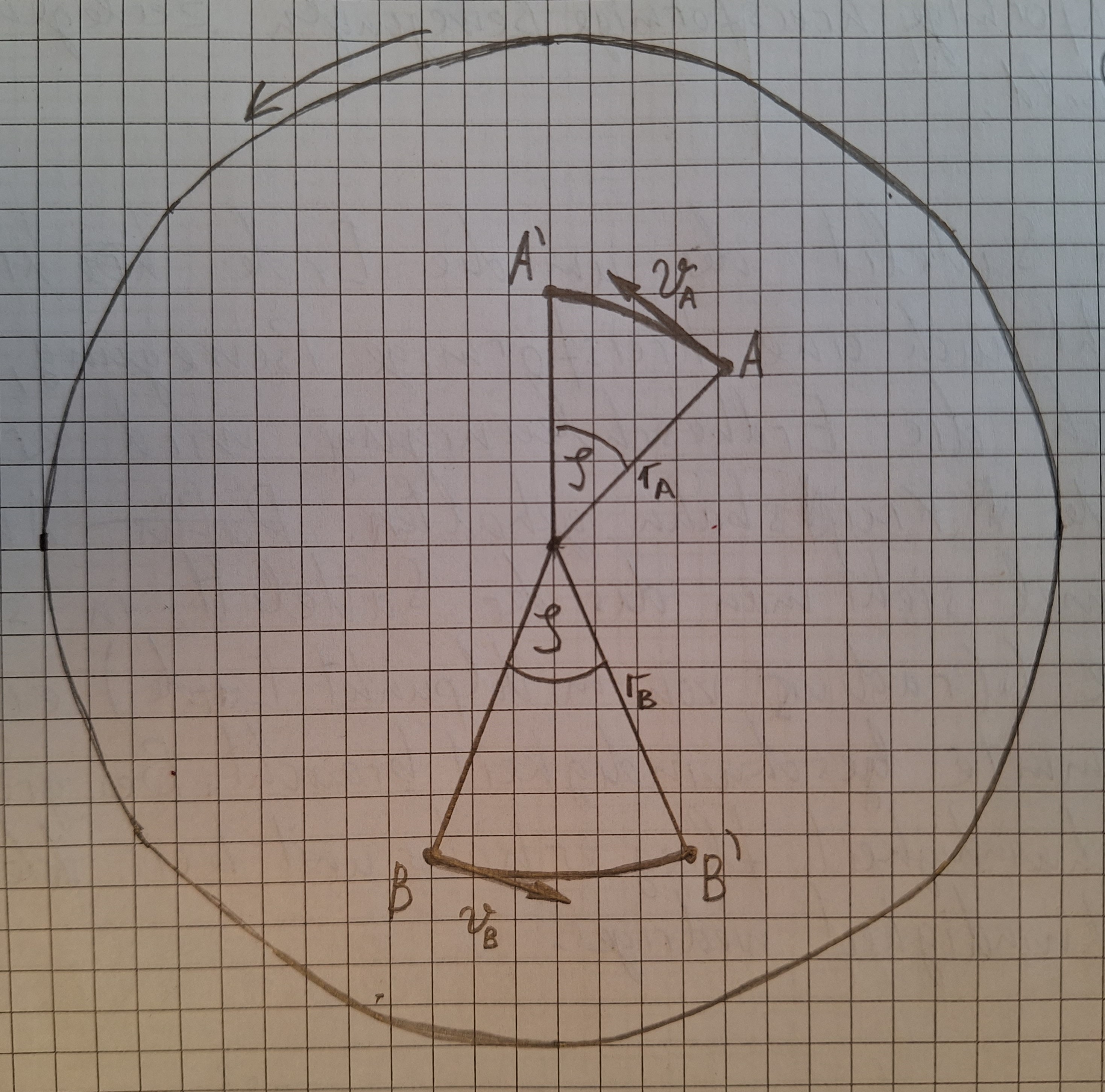
Ein Punkt bewegt sich von Ort A bis A' in der Zeit t. Die Geschwindigkeit ist VA. Ein anderer Punkt bewegt sich von Ort B bis Ort B' in der Zeit t. Die Geschwindigkeit ist VB. Die Zurückgelegte Strecke von den beiden Punkten ist verschieden, aber der Winkel φ der Drehbewegung ist gleich. Wenn sich der Körper z.B. um 30° gedreht hat, dann drehen sich alle seine Punkte um 30° (von Drehpunkt aus gesehen).
Das trifft nur auf starre Körper zu, nicht auf weiche oder flüssige. Bei einem weichen Körper kann z.B. eine Seite drehen und eine Seite feststehen.
Gleichförmige Drehbewegung ist, wenn in gleich großen Zeitabständen der Körper sich um gleich große Winkel dreht.
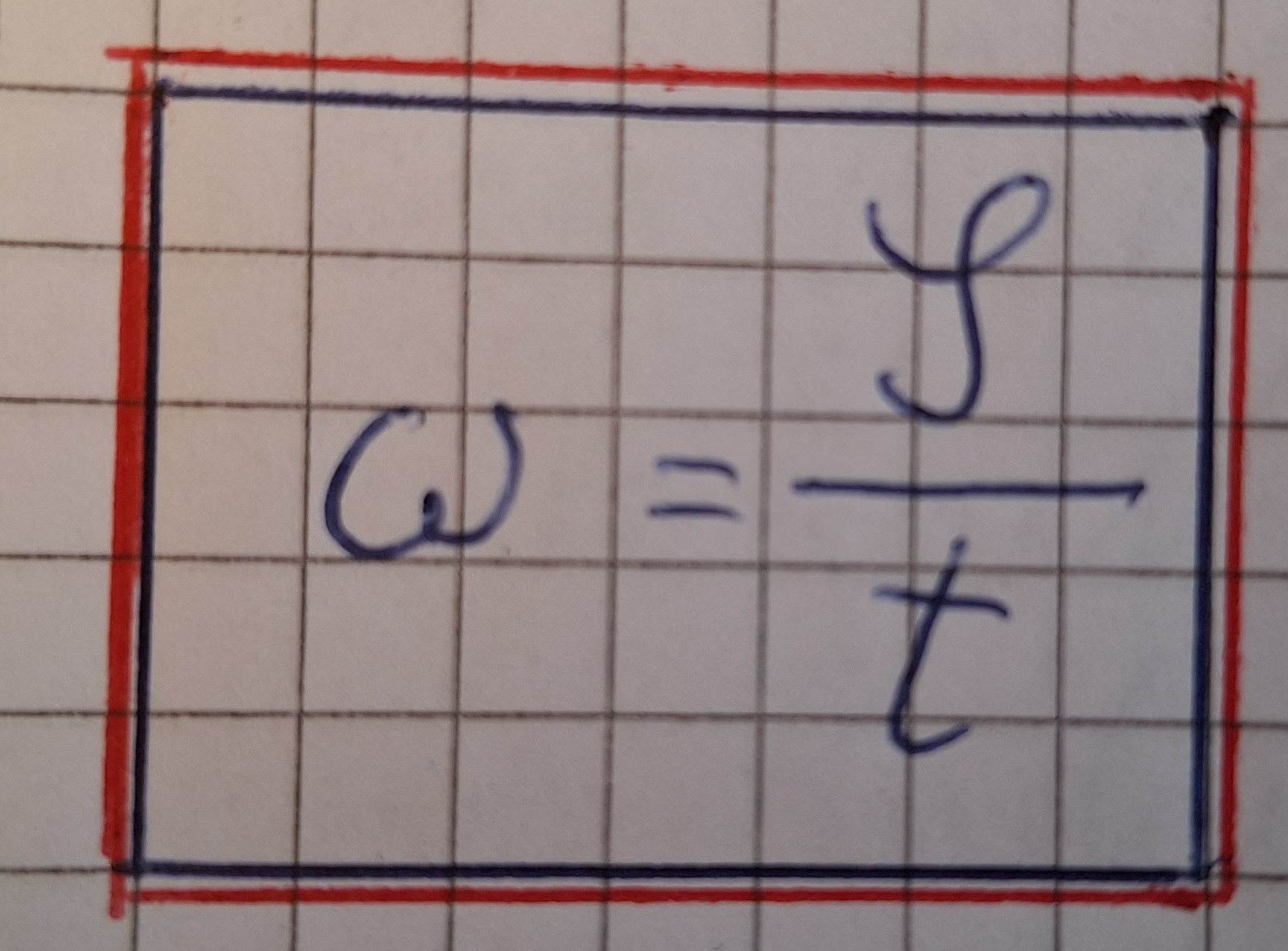
Omega (ω) ist gleich phi (φ) geteilt durch Zeit t.
Einheit:
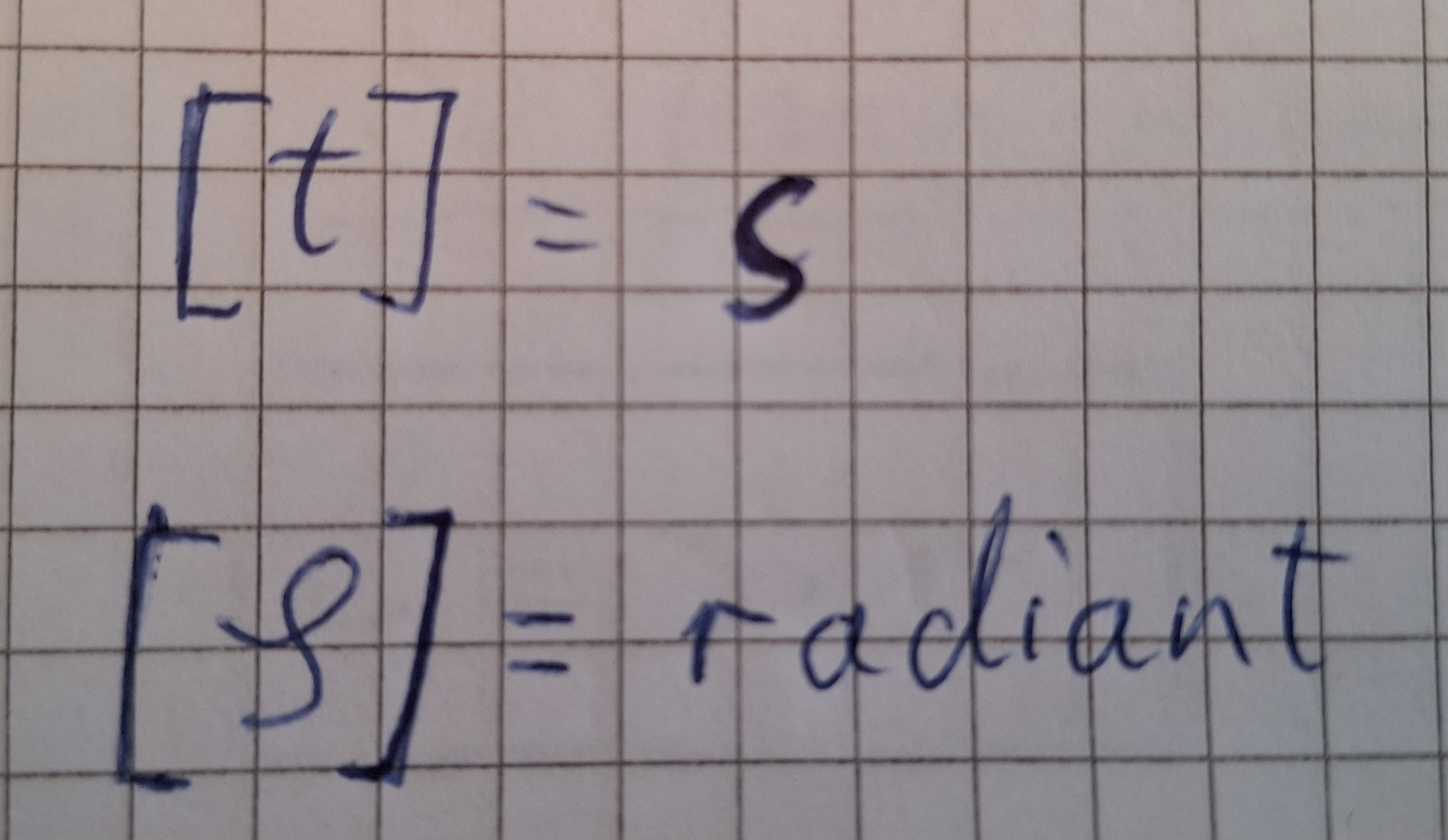
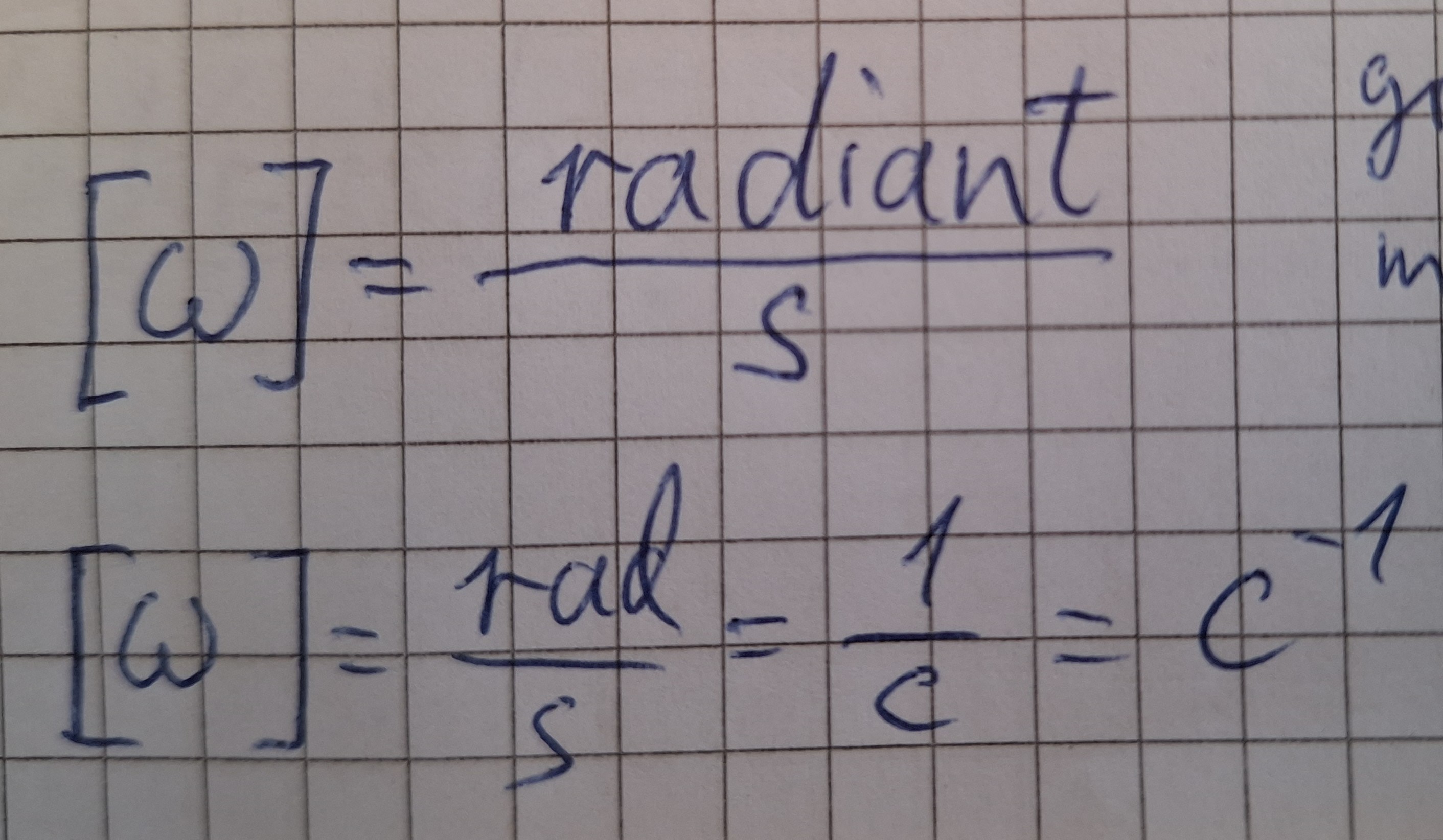
Zuerst die Erklärung von Radiant.
Radiant ist ein Winkelmaß, abgekürzt rad. Zeichnen wir einen Winkel das ein rad groß ist!
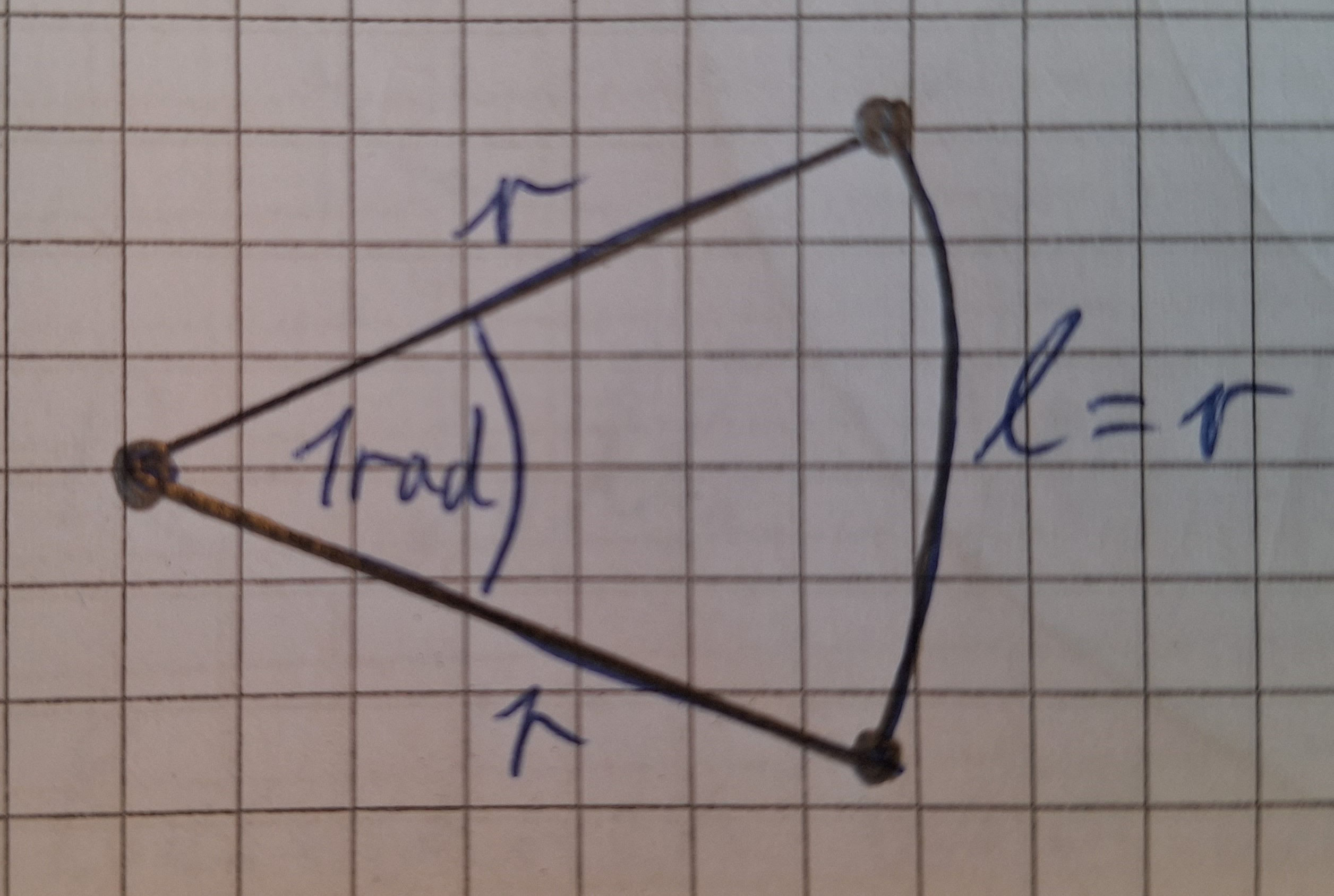
Bei dem Kreisausschnitt ist der Kreisbogen l genau so lang wie der Radius r. Bei einem rad ist der Kreisbogen l gleich lang dem Radius r.
Ein Radiant ist der Winkel von einem Kreisausschnitt, dessen Kreisbogen so lang ist wie der Radius.
Wenn
- l = r dann 1 rad
- l = 0,5 r dann 0,5 rad
- l = 0,1 r dann 0,1 rad
- l = φ r dann φ rad
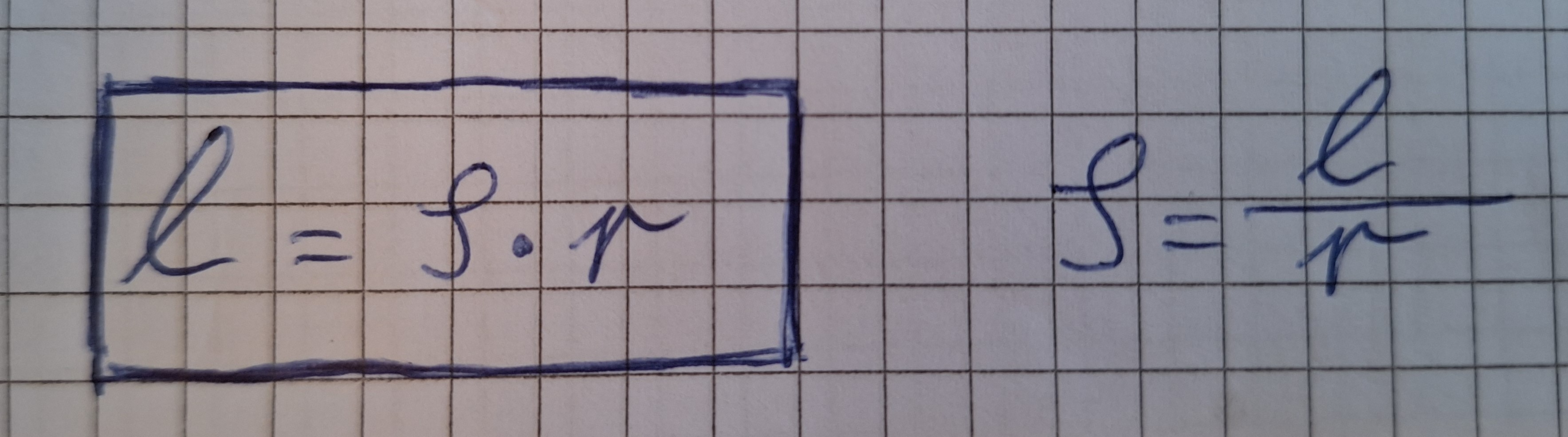
Daraus kann man die Formel, um den Kreisbogen l zu berechnen, ableiten.

Vollwinkel oder der volle Winkel
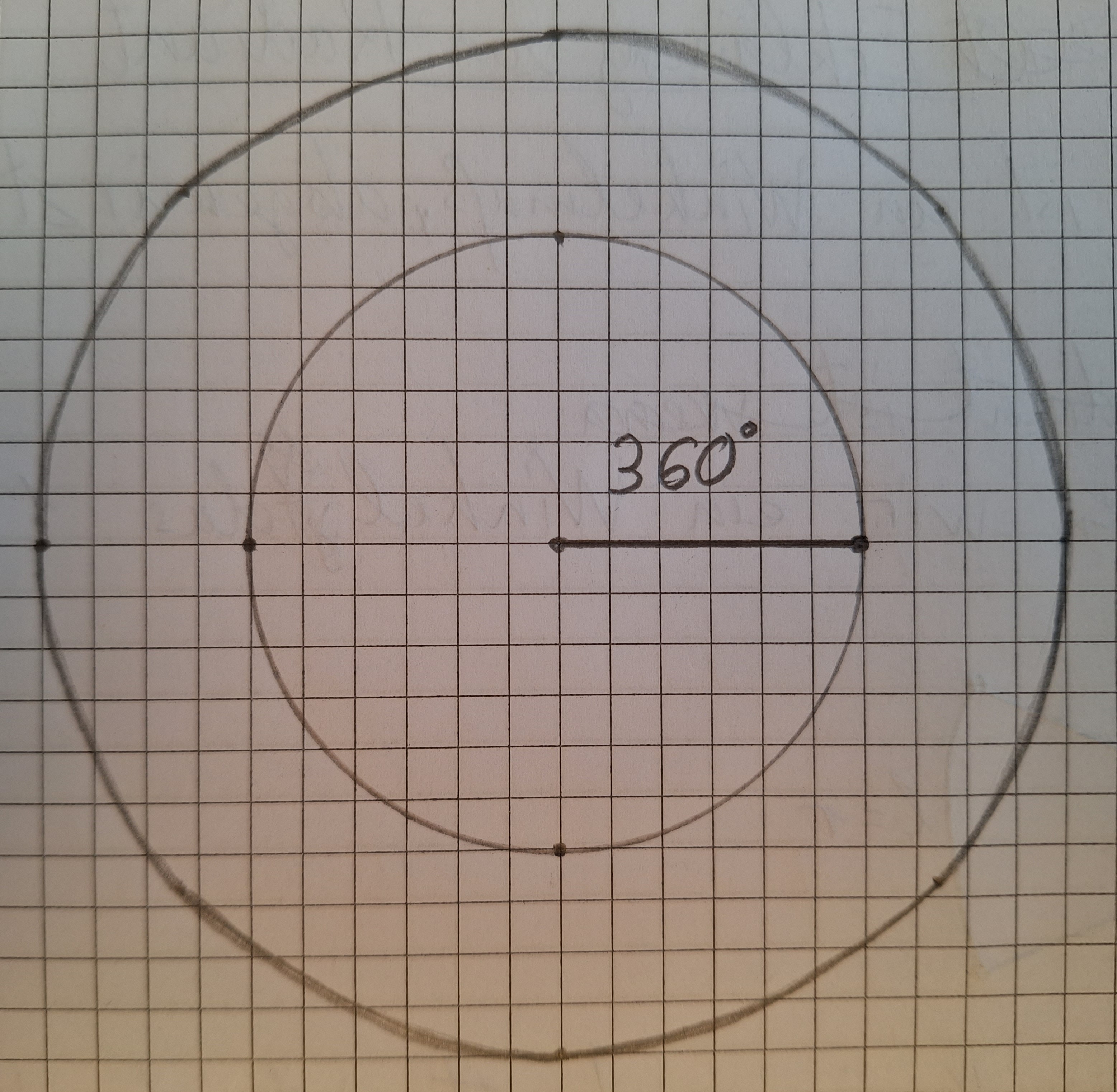
Der volle Winkel hat 360°.
Berechnen wir das in Radiant.
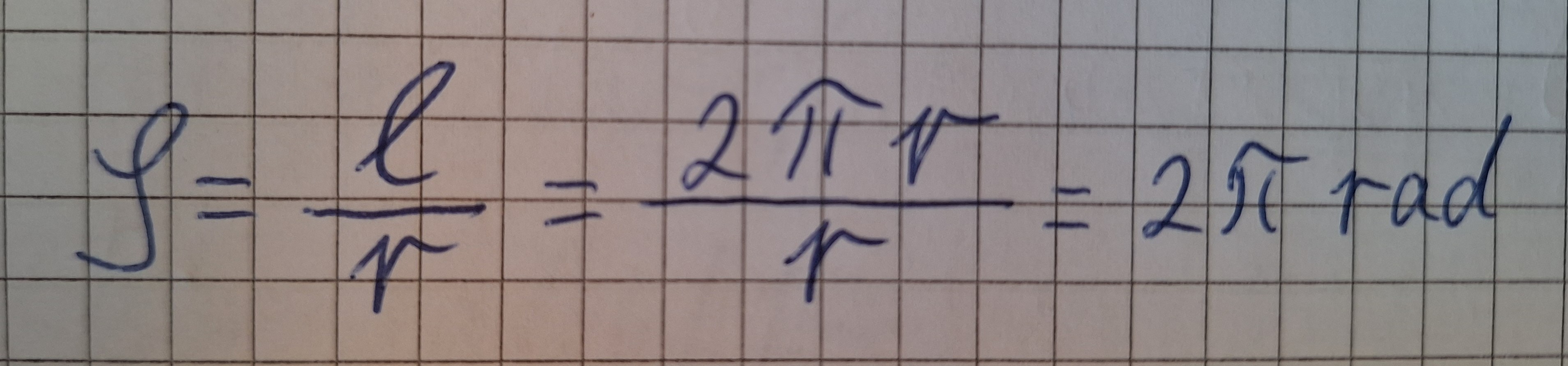
360° = 2*π rad.
Grad in Radiant

Ein Radiant ist ca. 57,3° Grad.
Bahngeschwindigkeit (Tangentialgeschwindigkeit) Formel Herleitung
Nehmen wir die Formel
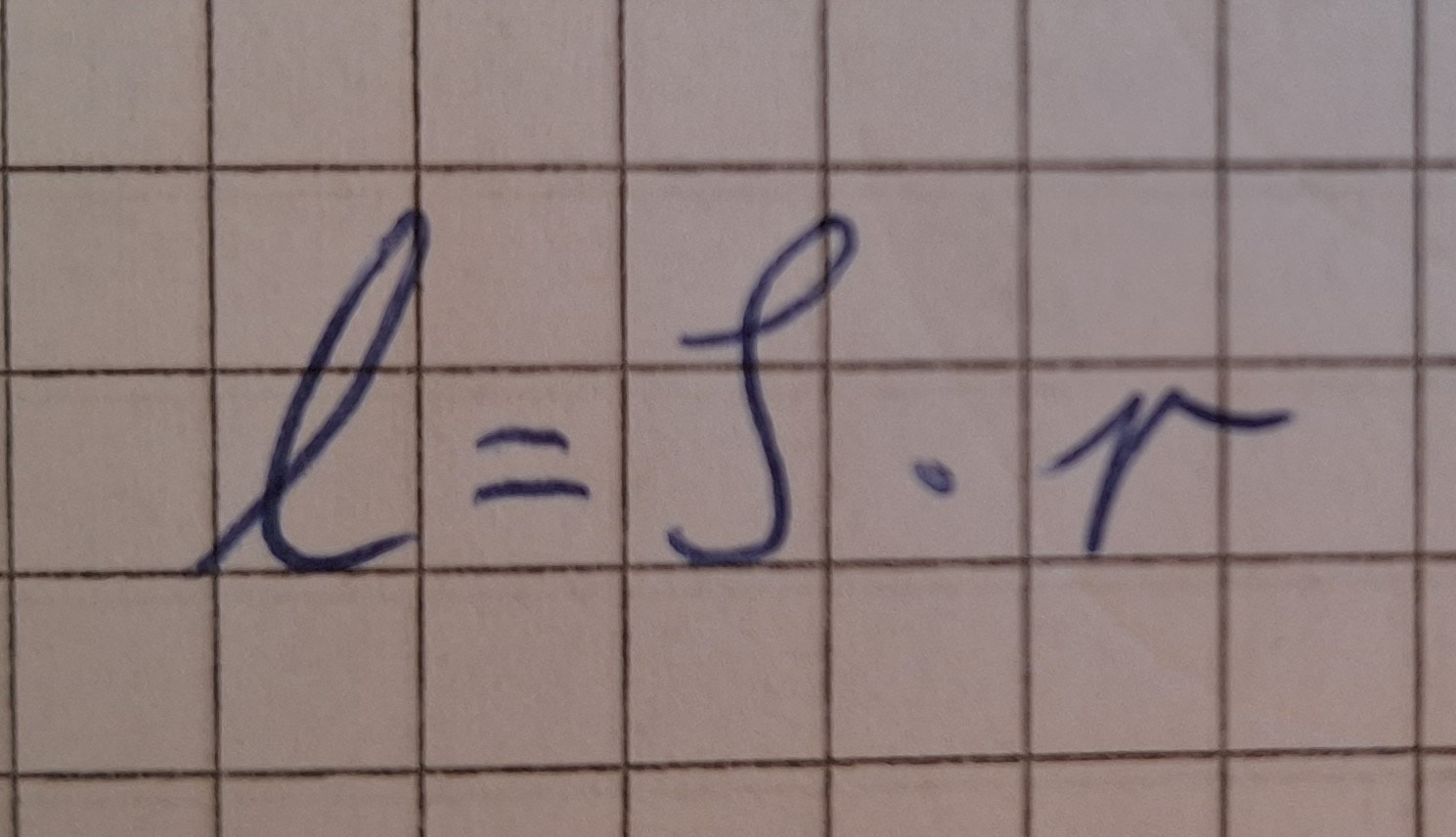
Eine gleichförmige Drehbewegung von A nach B, Bogenlänge ist l, und Kreisbogenwinkel ist φ.
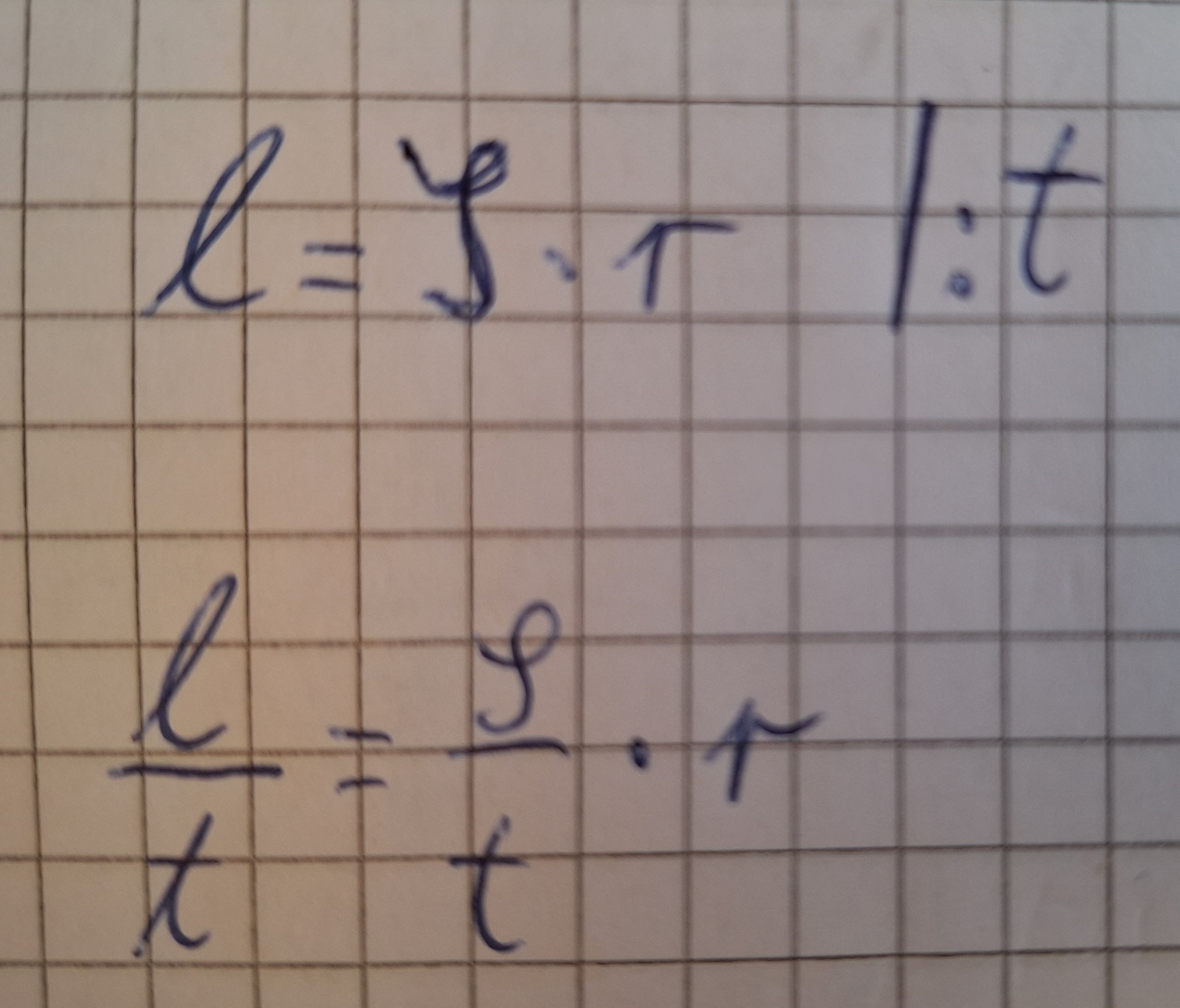
Da l/t=v und φ/t=ω .
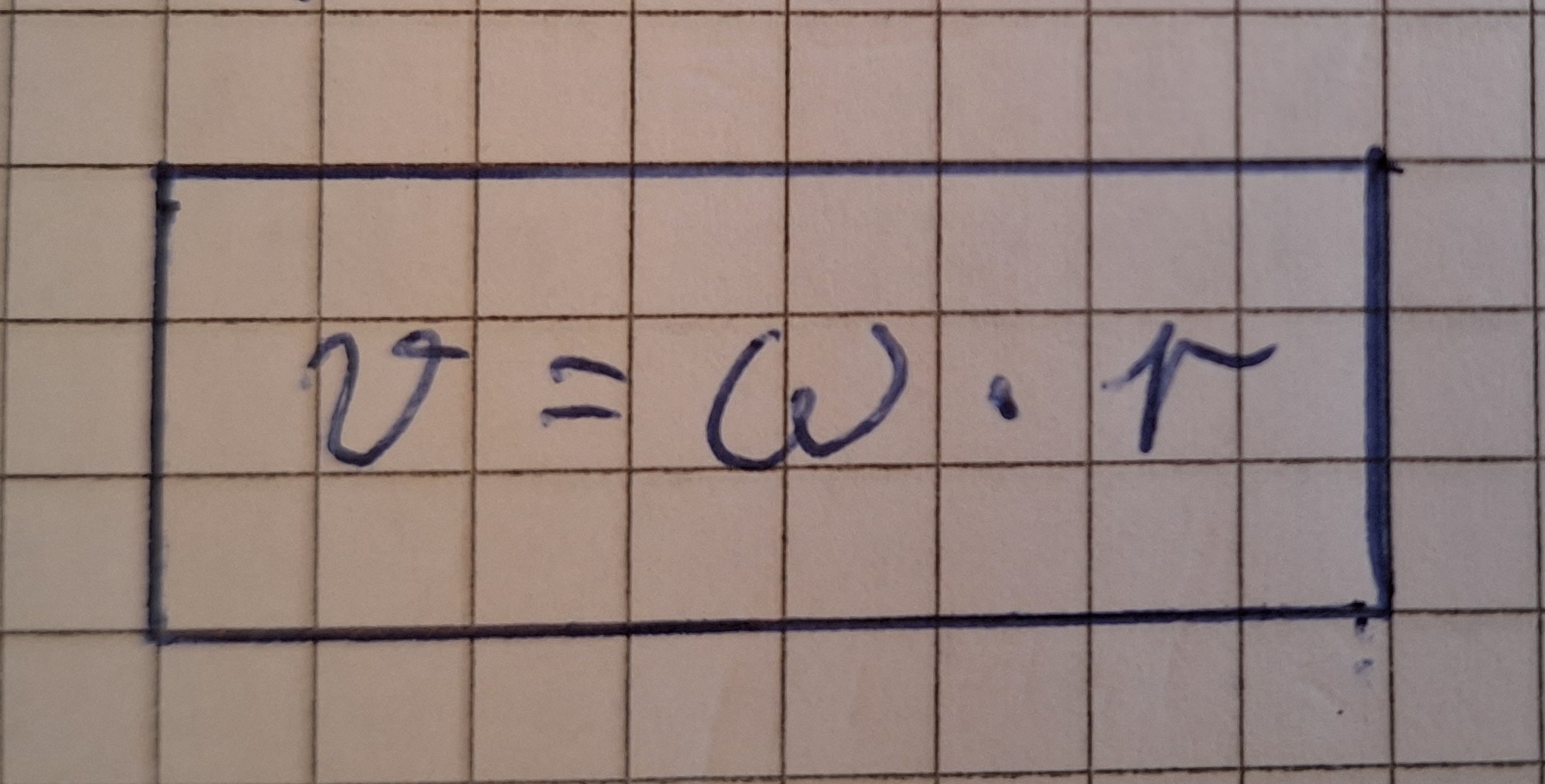
Periode der Drehbewegung
T - Periode
n - Frequenz
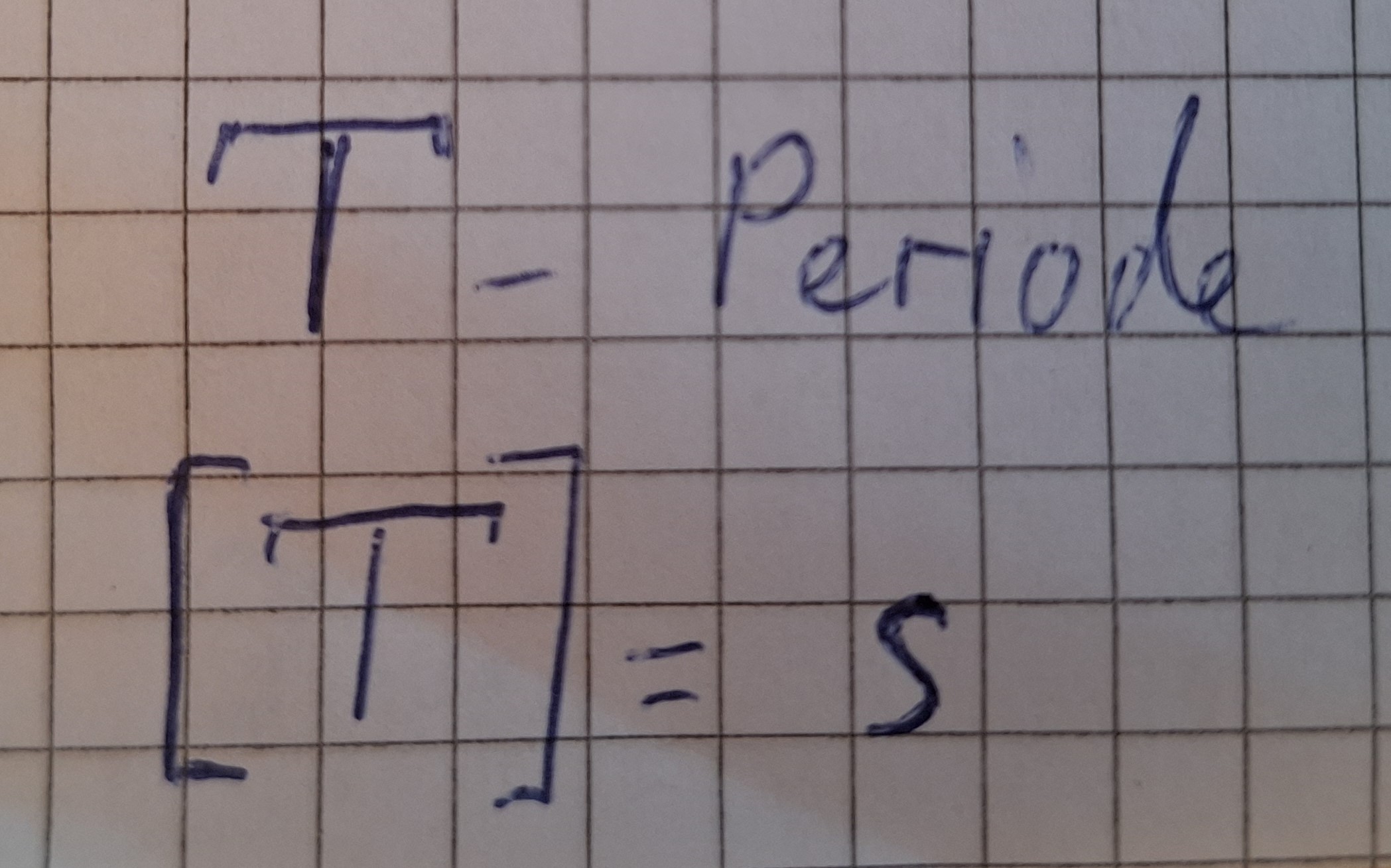

Periode (T) dauer einer Umdrehung in sec.
Frequenz n anzahl der Umdrehungen pro sec.
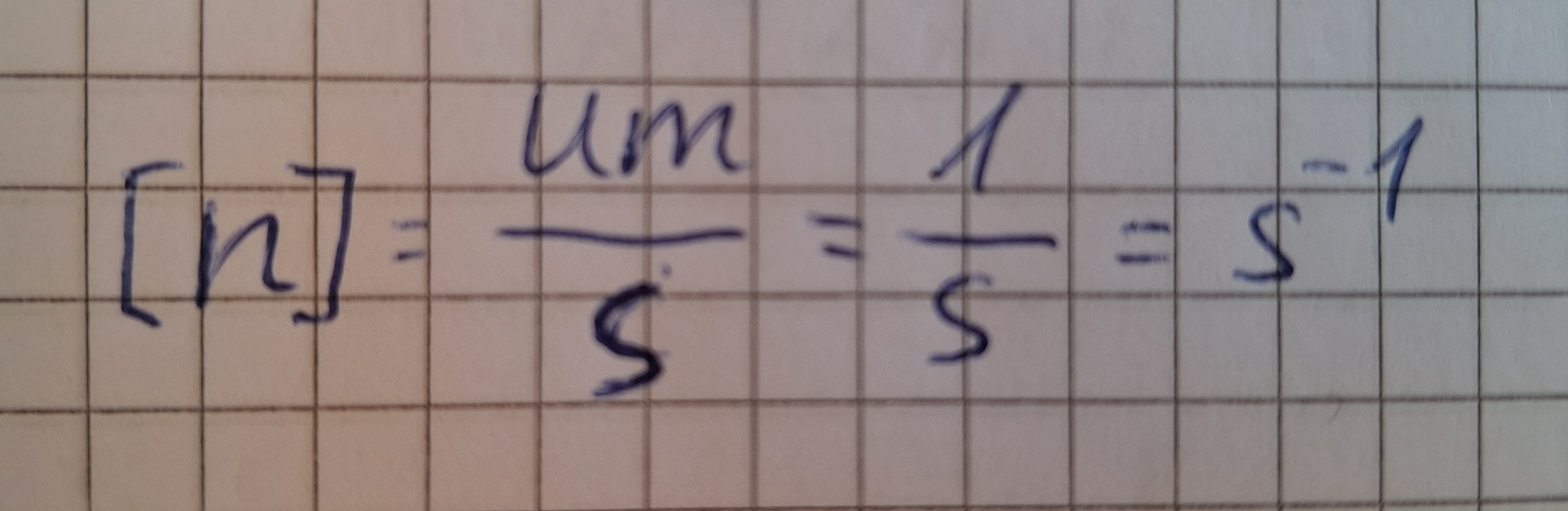
Um die Periode zu berechnen, muss man die Zeit durch die Anzahl der drehungen N (in der Zeit t) teilen.
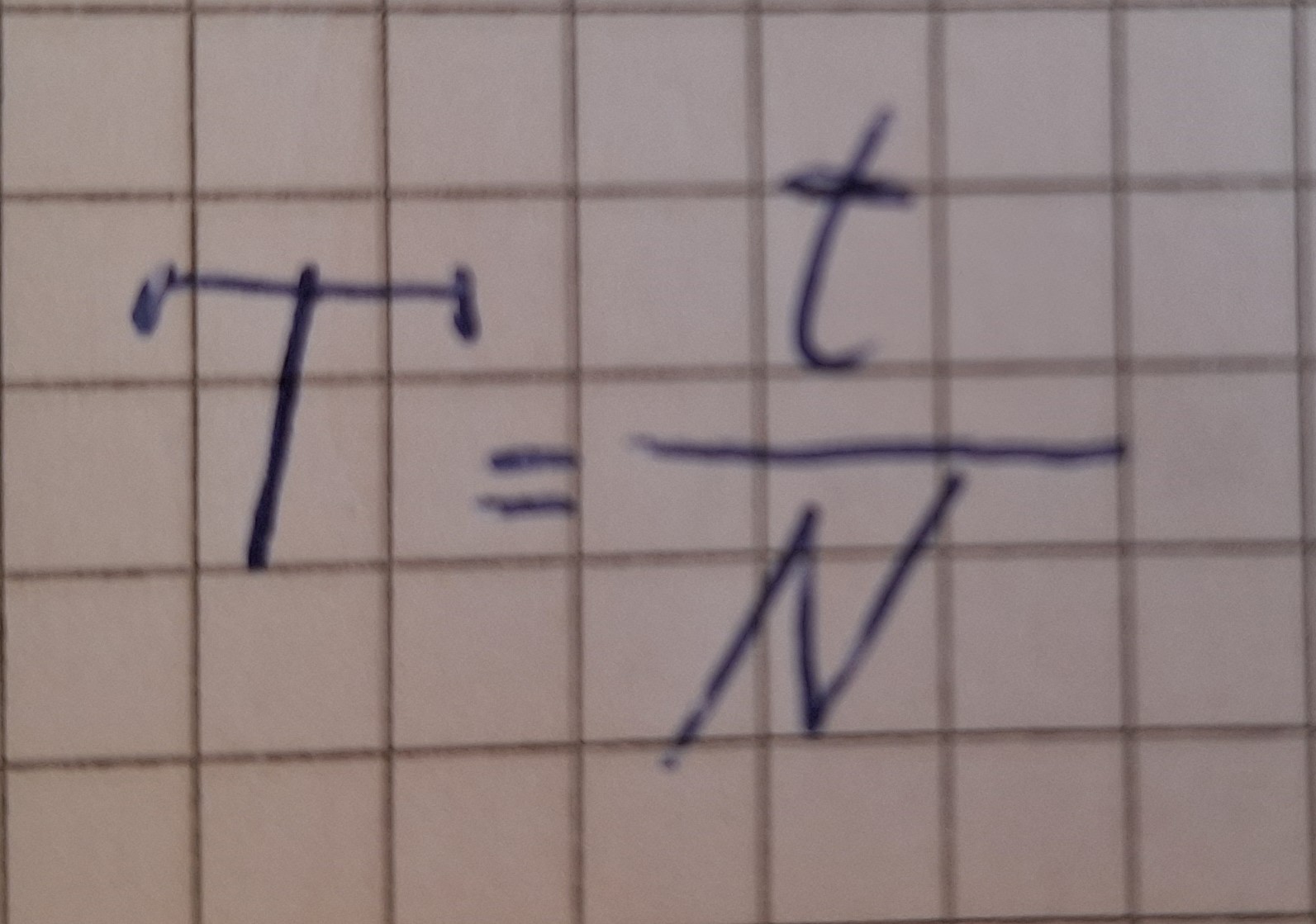
Um die Frequenz zu berechnen, muss man die Anzahl der Drehungen N durch die Zeit t teilen.
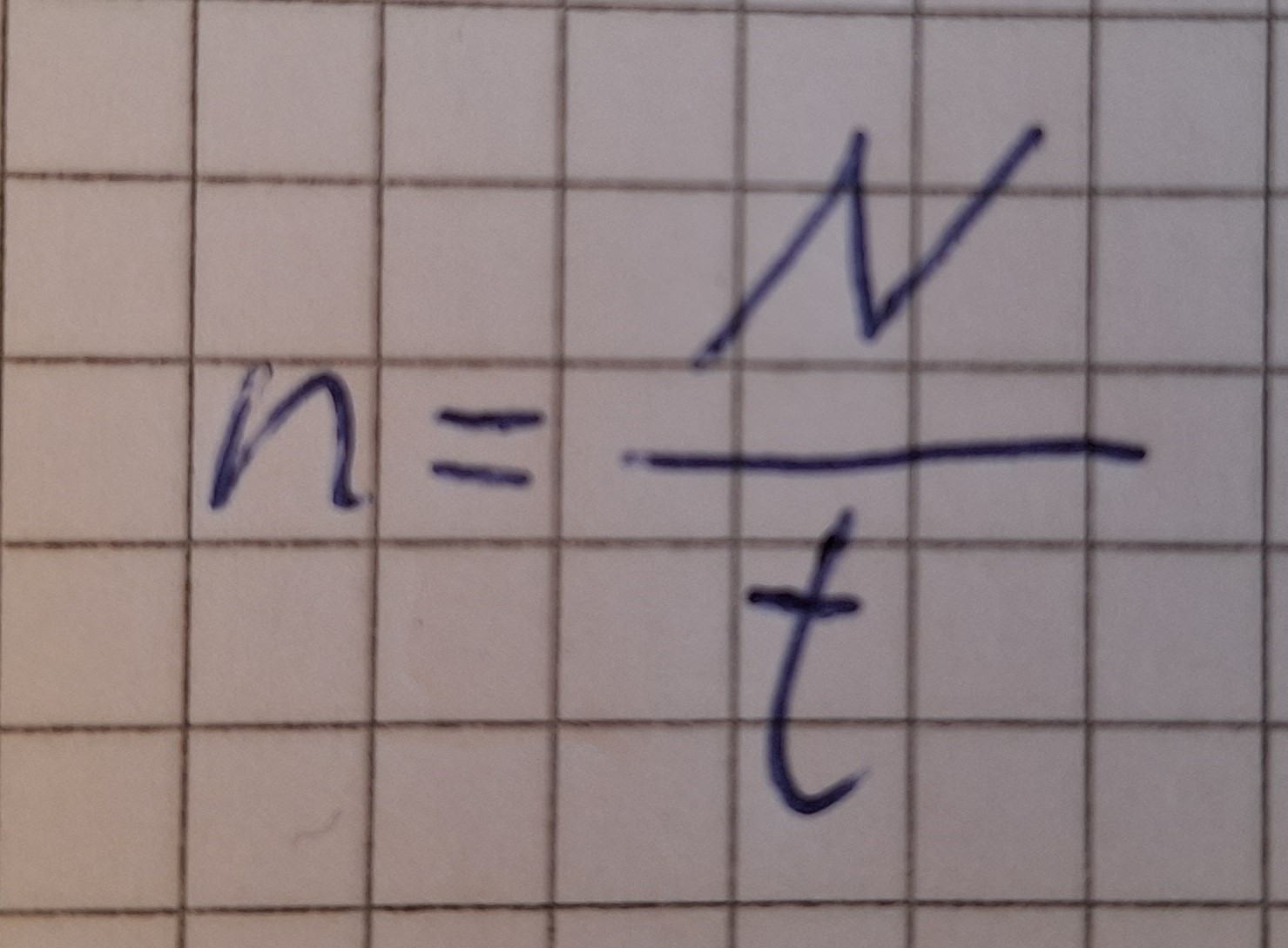
Man sieht.
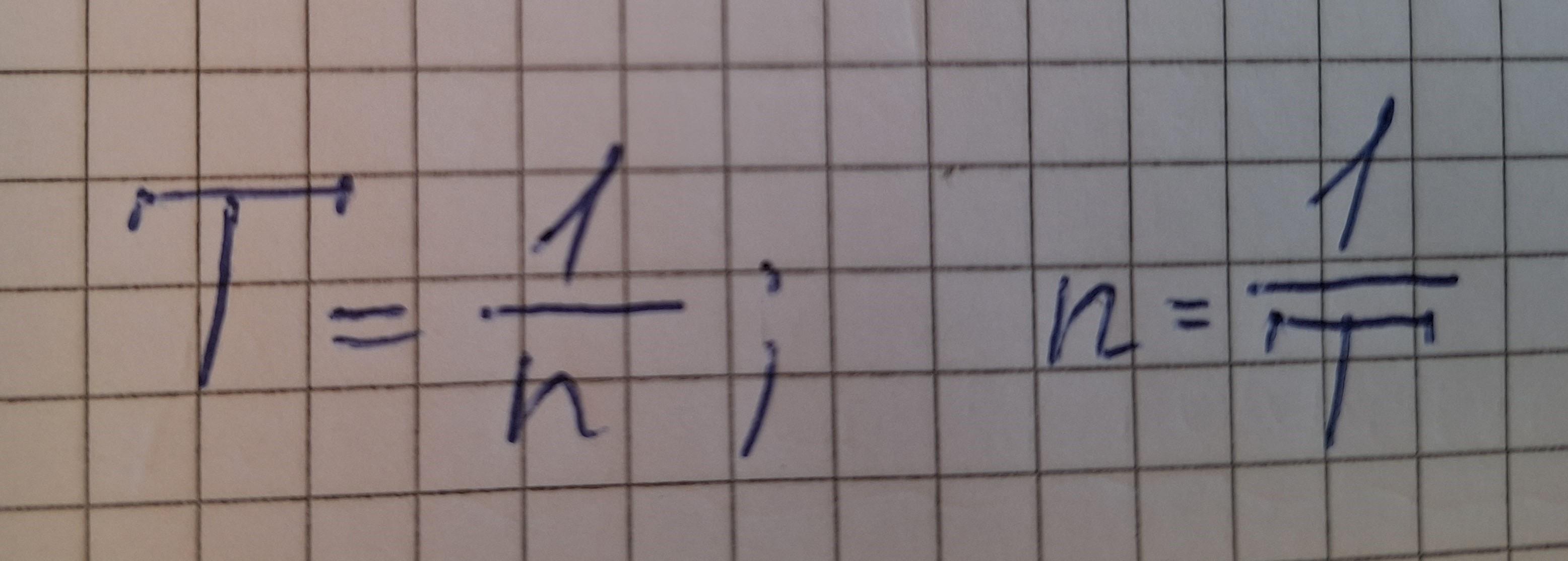
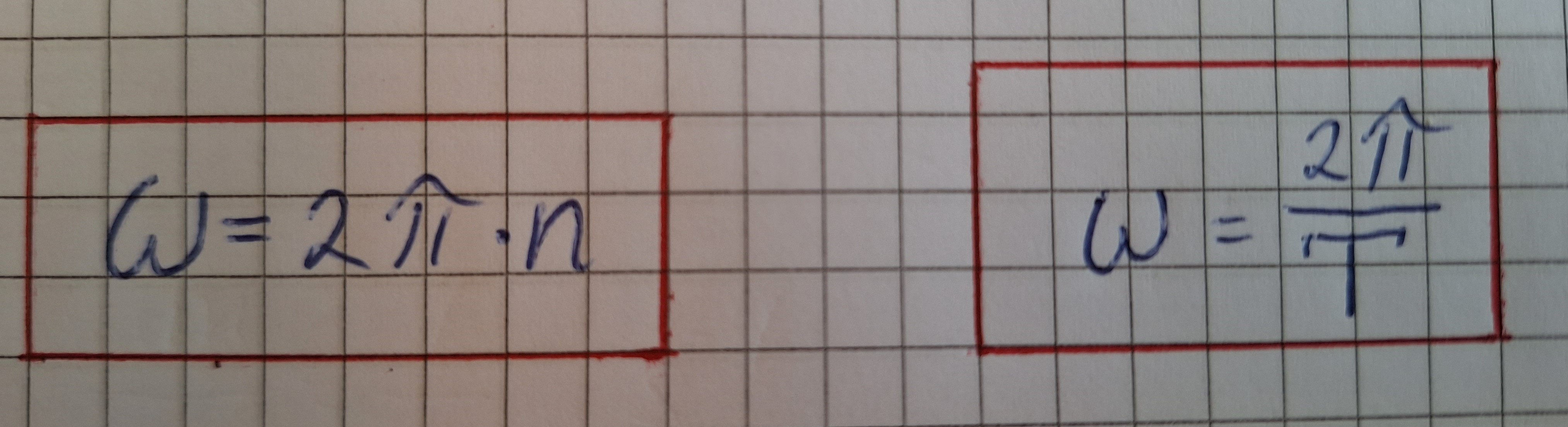
Eine Umdrehung sind 360° und in Radiant 2π rad.
Zwei Umdrehungen sind 2π * 2 rad.
3 Umdrehungen sind 2π * 3 rad usw.
Daraus entsteht die Formel für die Winkelgeschwindigkeit.

Formel mit Winkelgeschwindigkeit und Radialbeschleunigung

Formel einsetzen
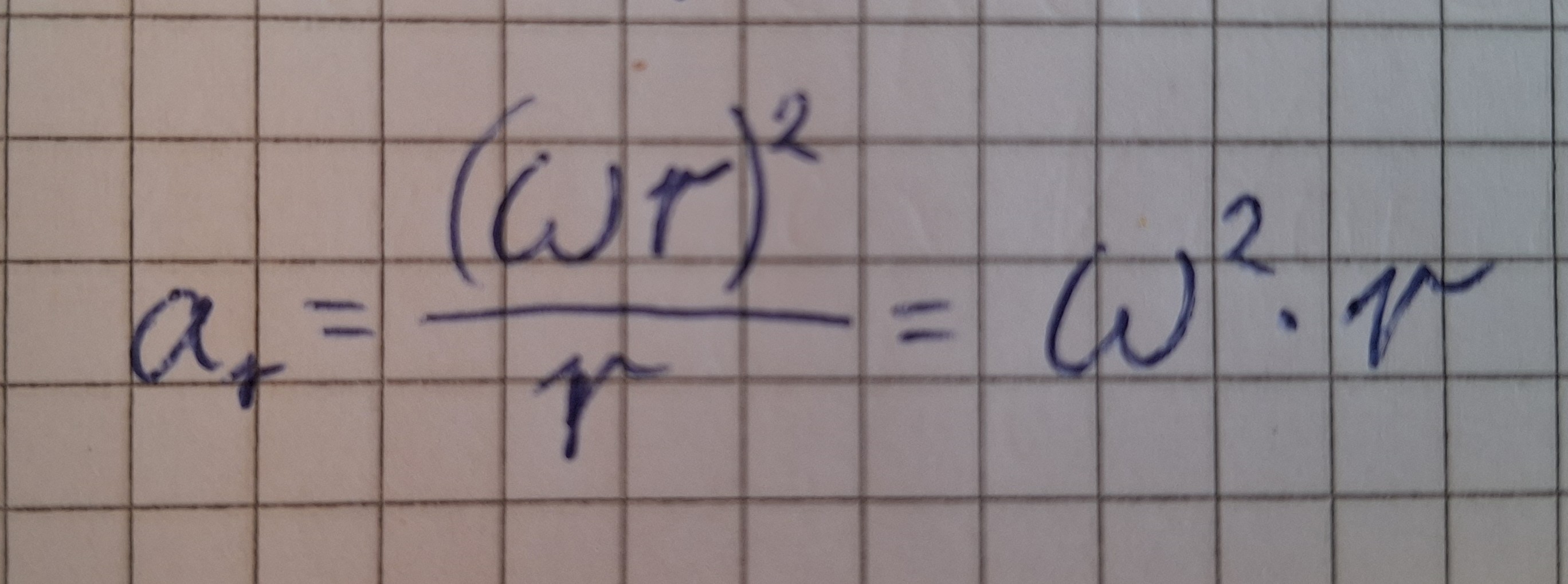
Radialbeschleunigung Formel: