Formelzusammenfassung:

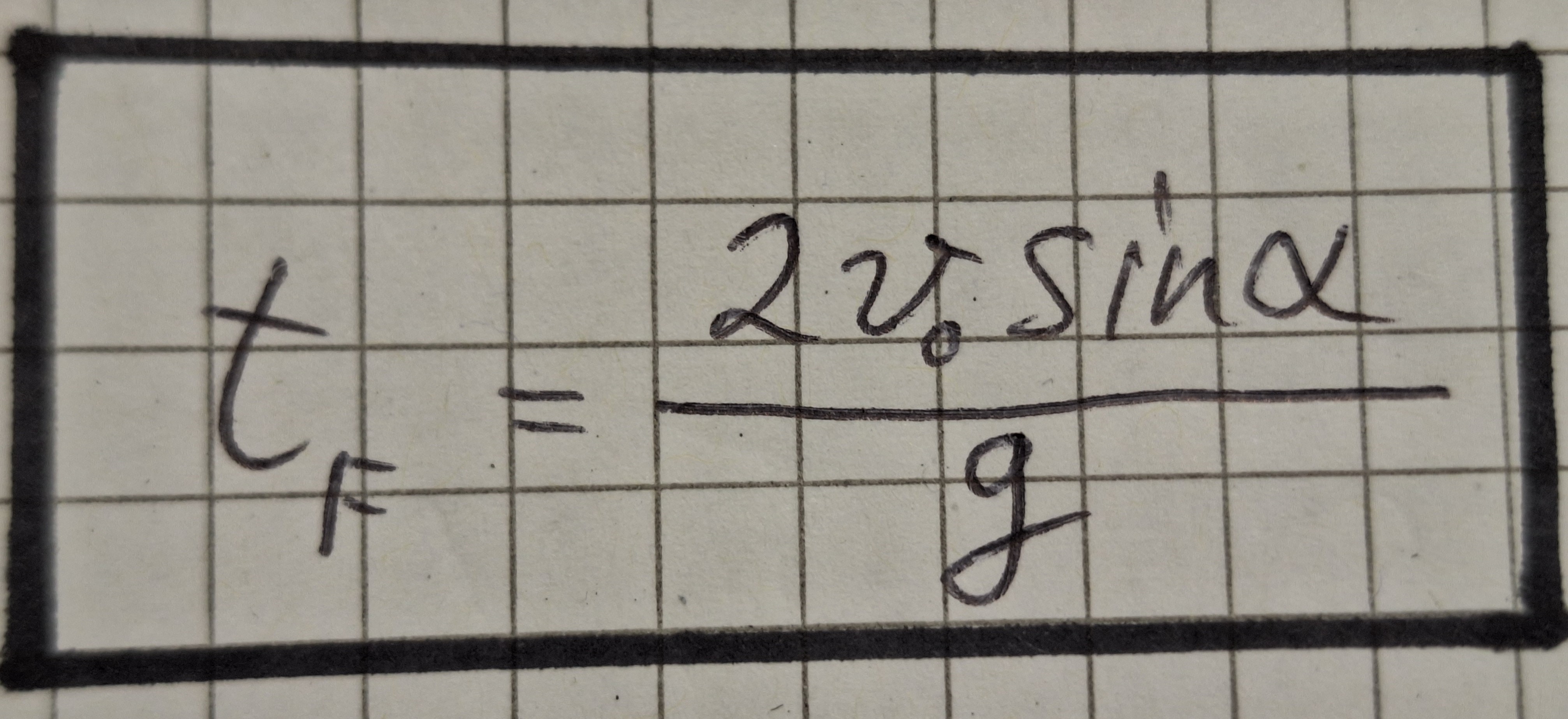
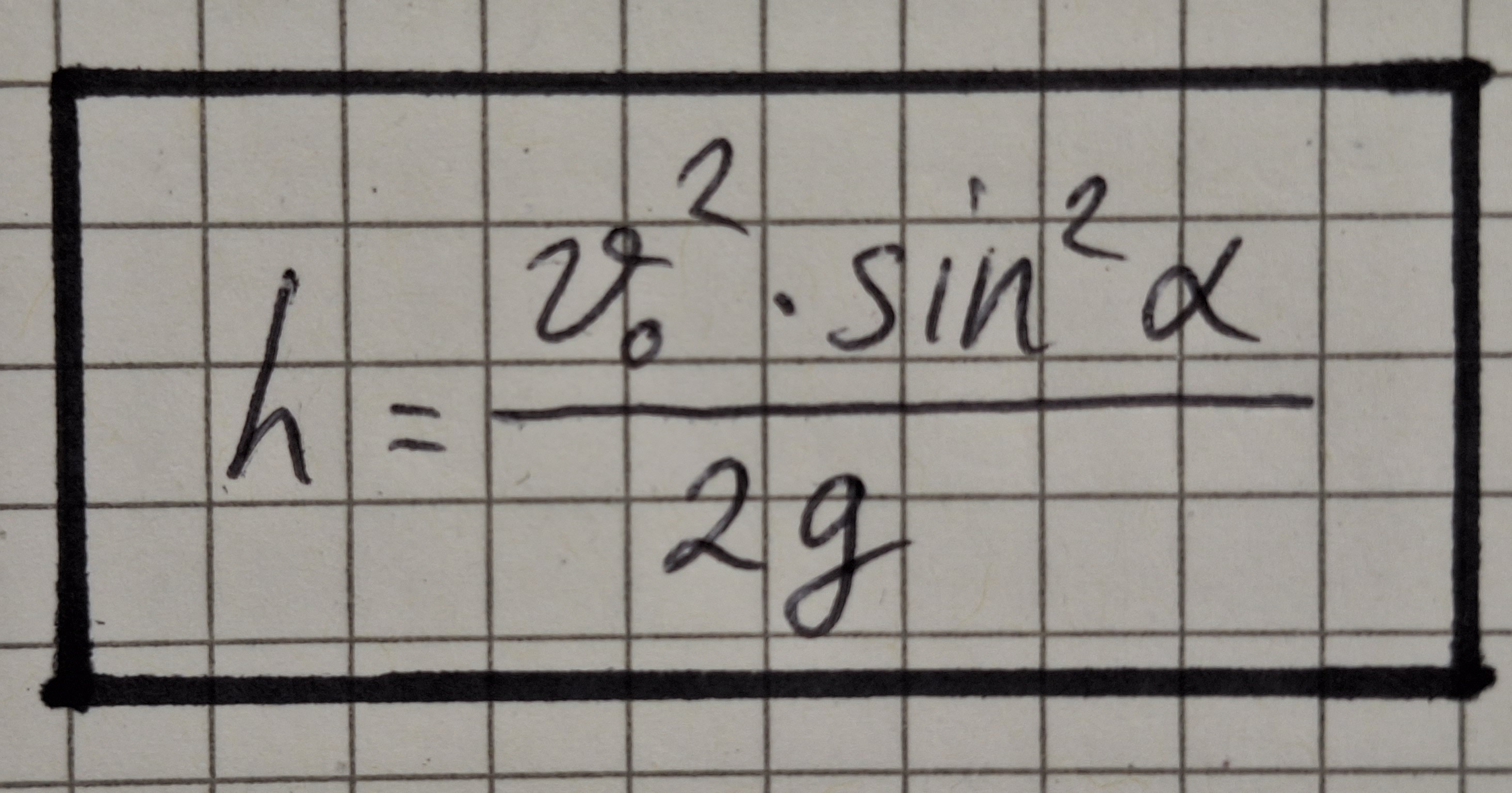
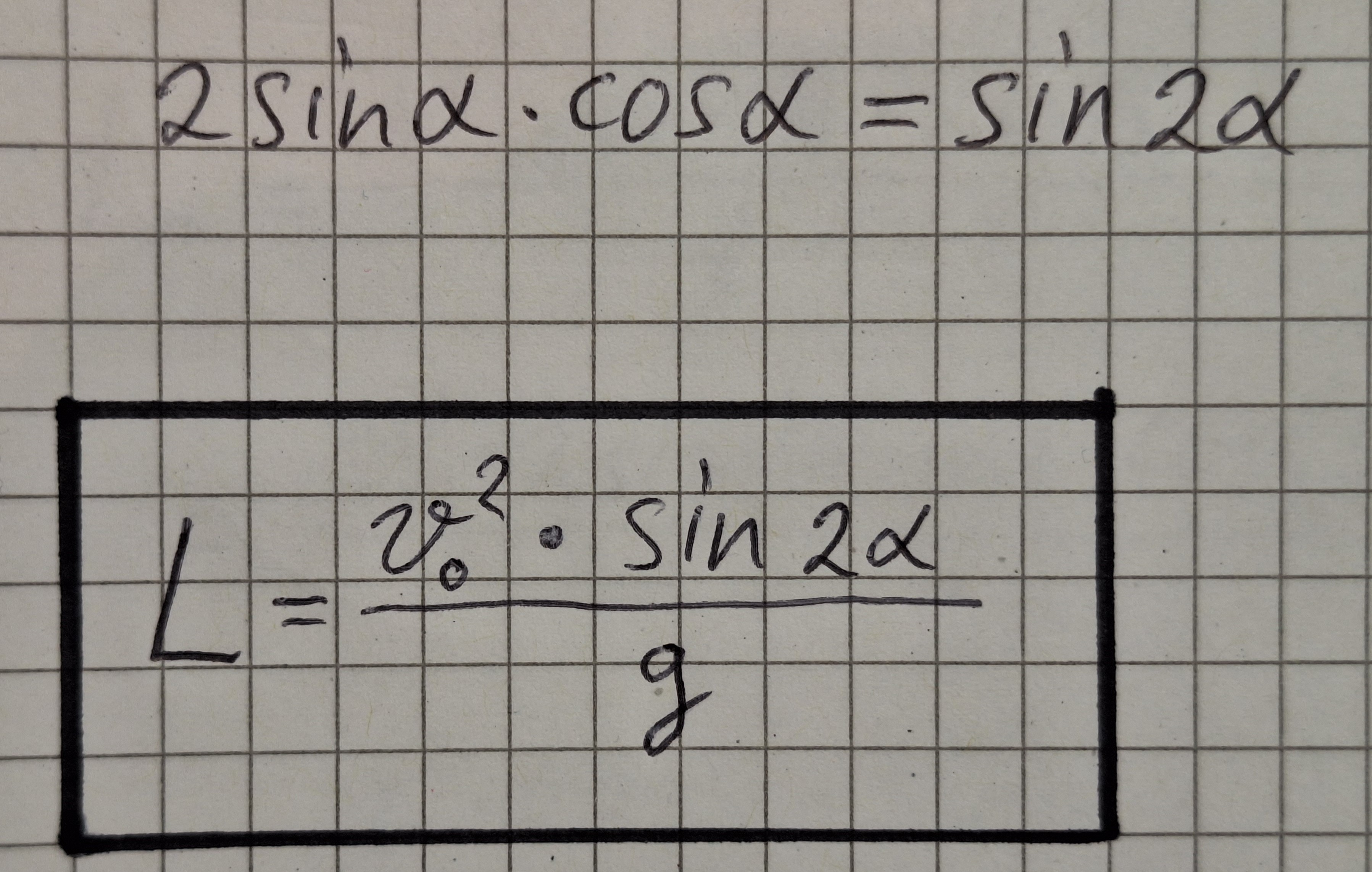
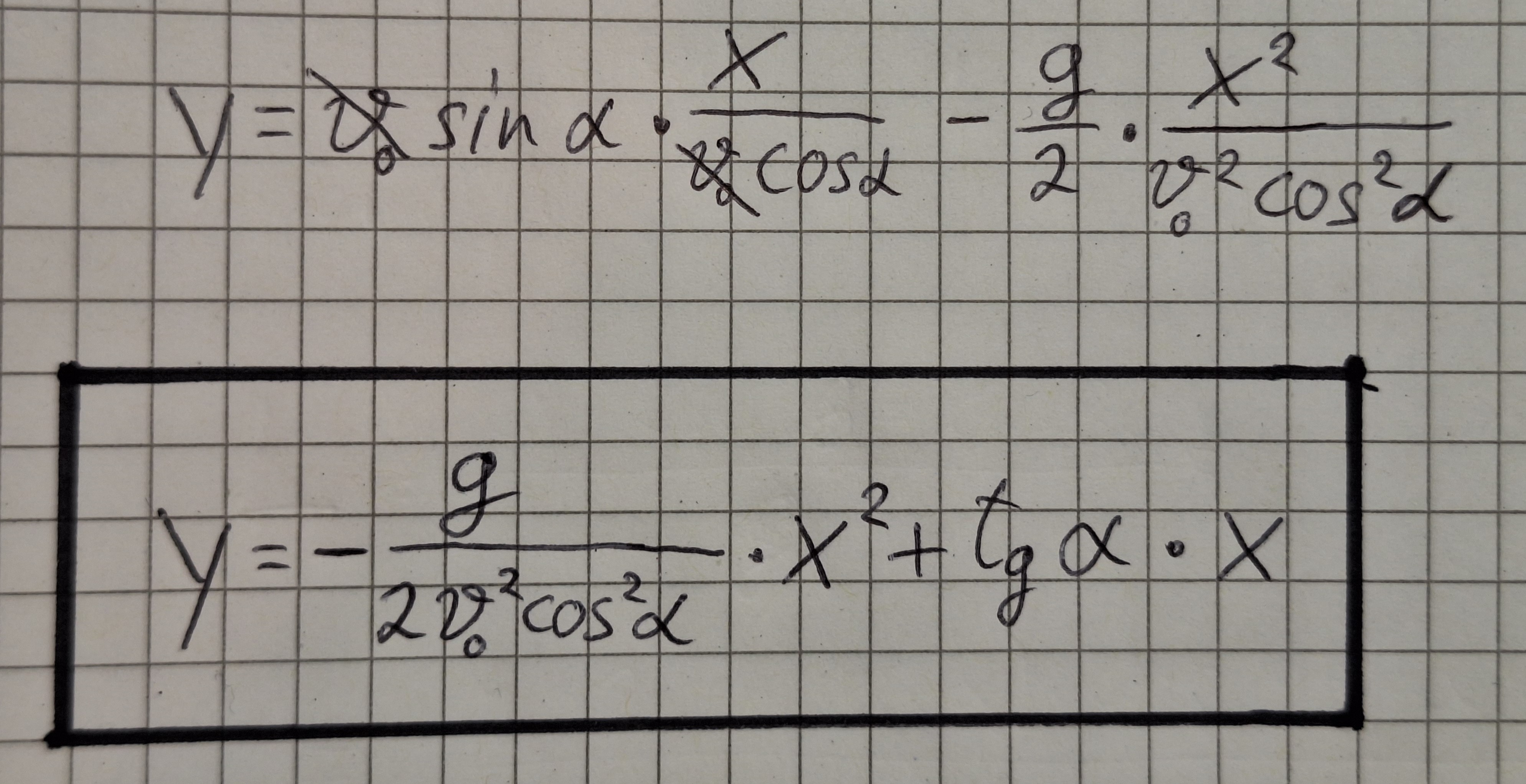
Freier Fall, Beschleunigung, mit Winkel.

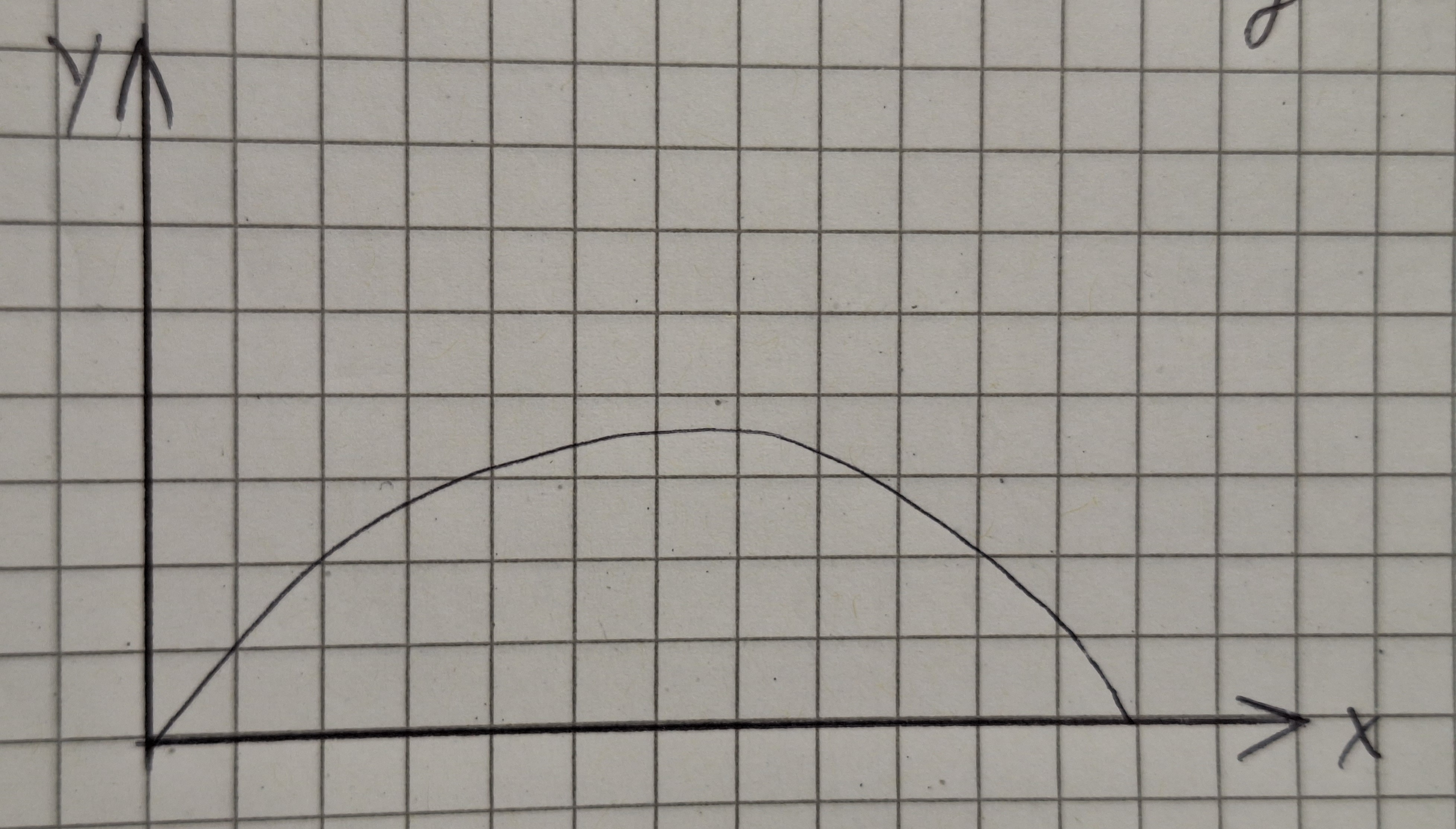
Hier erkläre ich die Flugbahn eines Körpers der mit einem Winkel zur Erde geworfen wurde. z.B. Das Werfen eines Steins in den Horizont.

Bei den Berechnungen wurde der Luftwiderstand nicht berücksichtigt.

Berücksichtigt wurde auch nicht das die Erde rund ist. Da der Beschleunigungsvektor zum Zentrum der Erde zeigt und an verschiedenen stellen verschiedene richtungen dann hat.

Dazu brauchen wir.

Beschleunigung a ist die Fallbeschleunigung g.

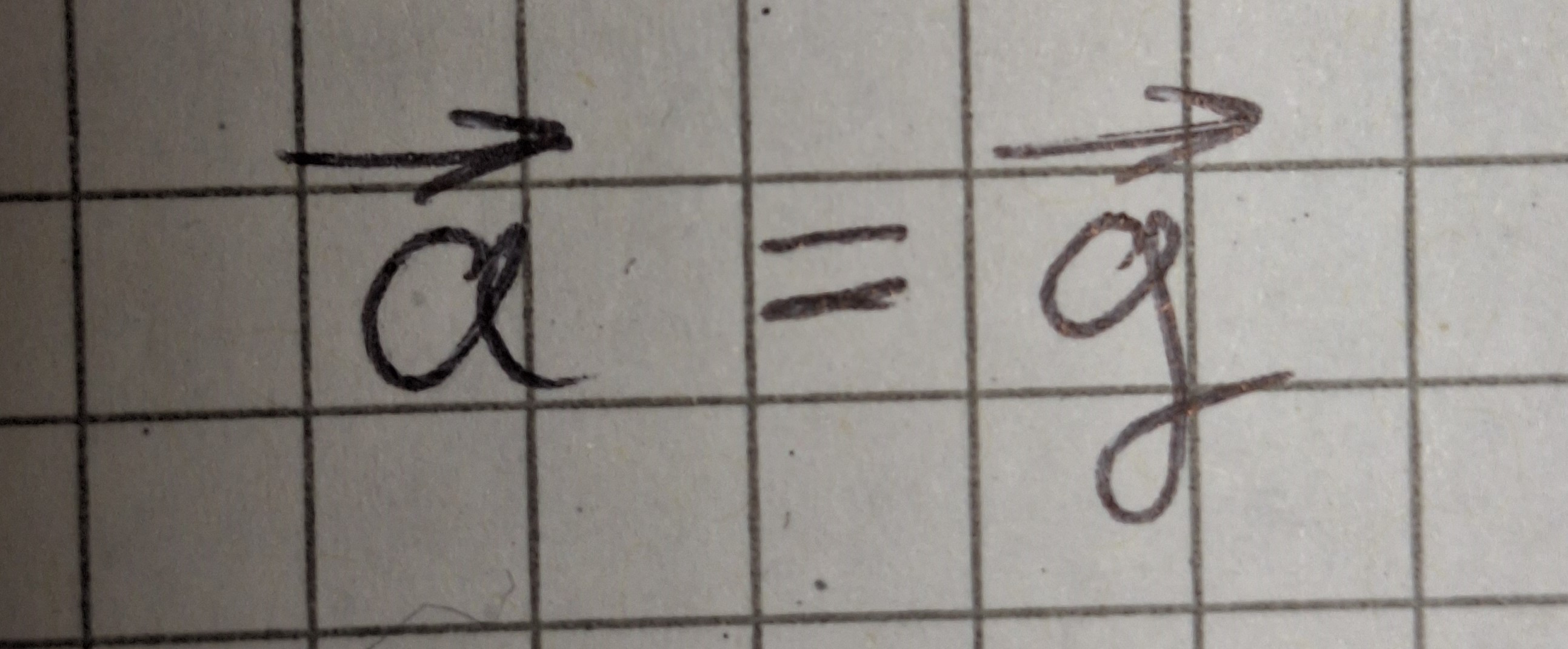
Formel von der Bewegung eines Körpers.

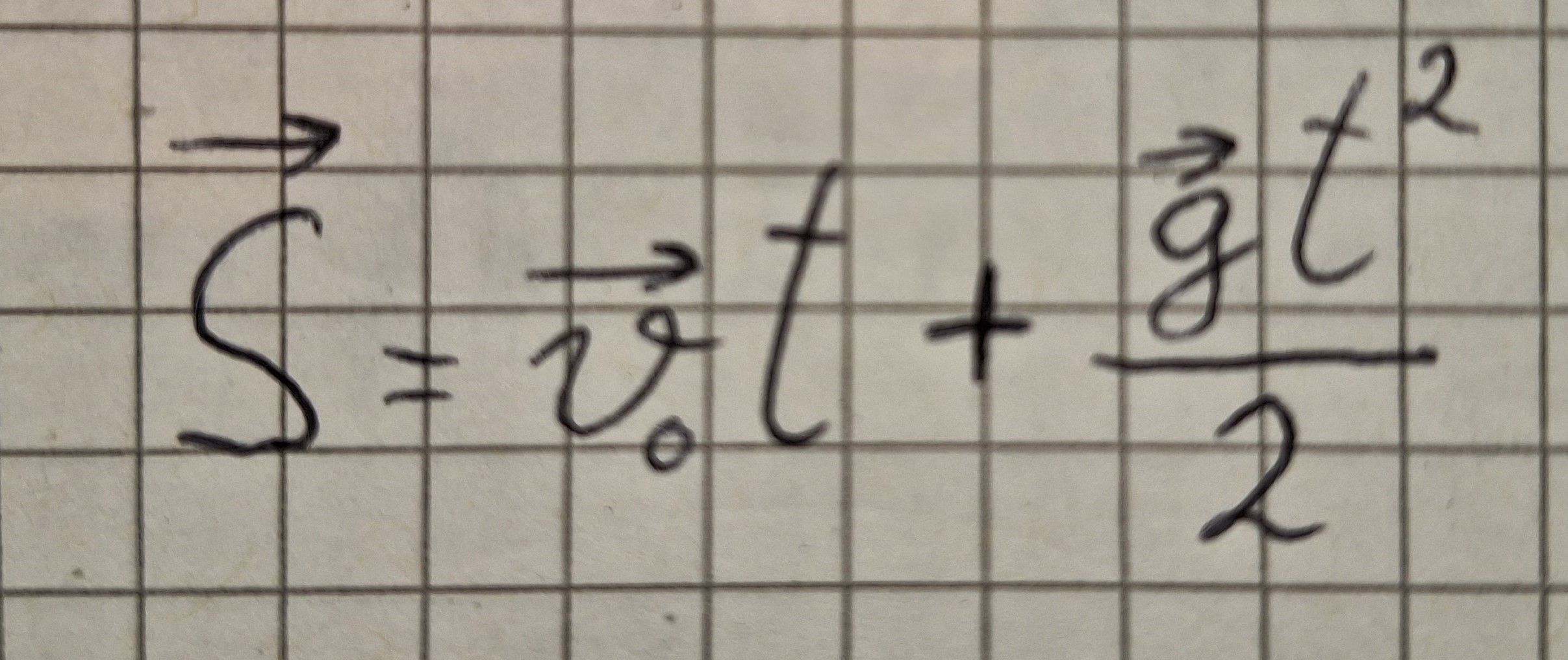
Und Formel der änderung der Geschwindigkeit.

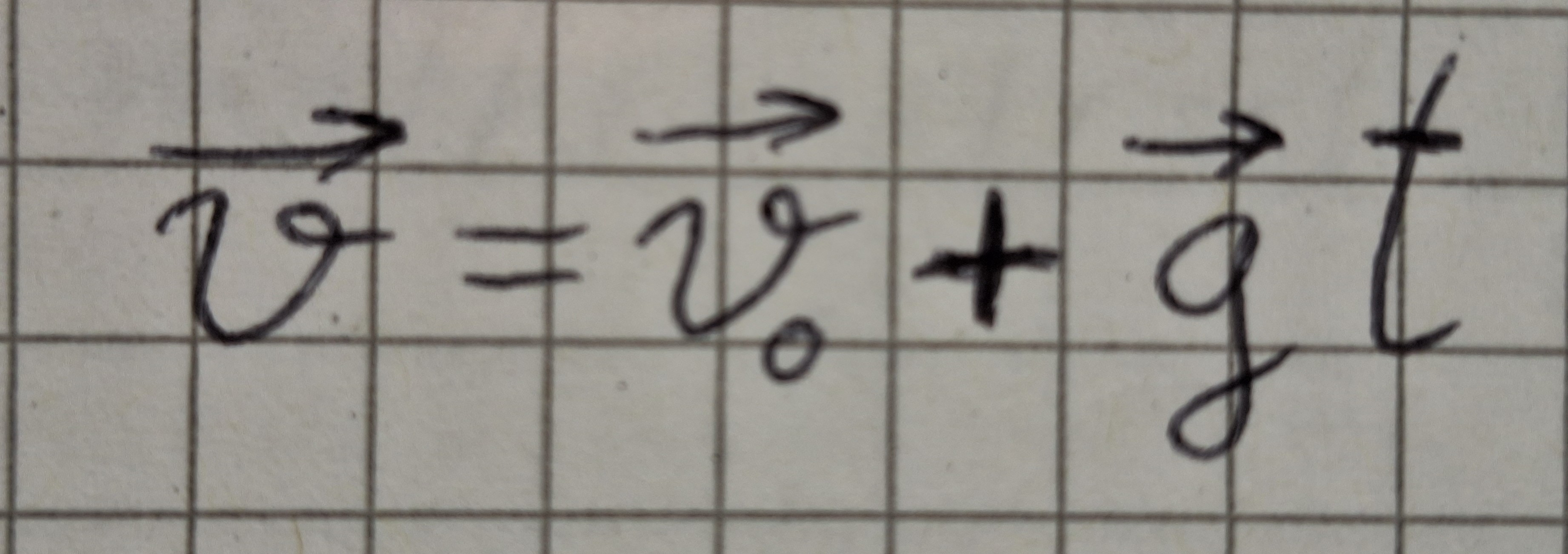
Beispiel:

Ein Körper wird geworfen, mit einem Winkel zur Erde.

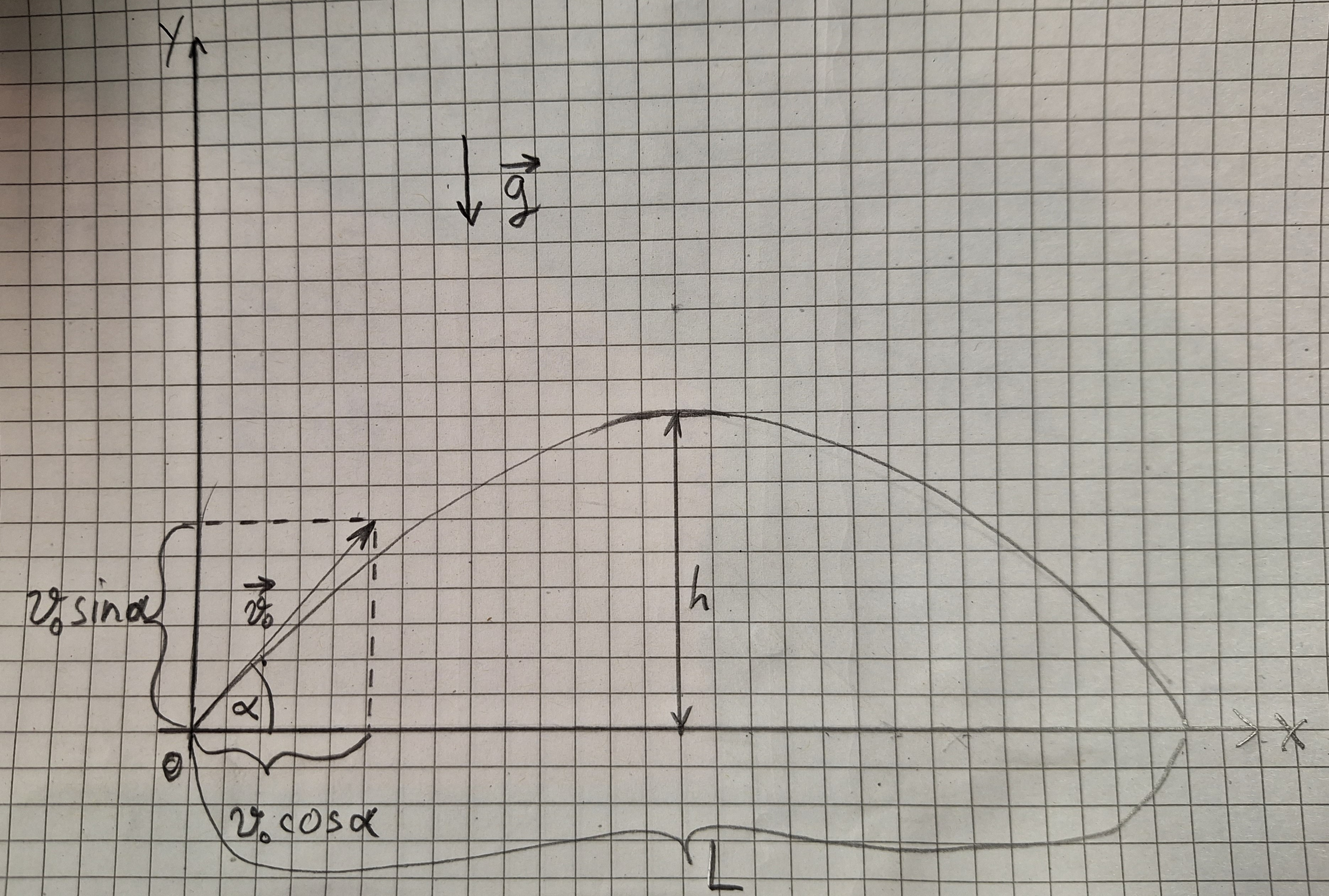
Gegeben:

v₀(Anfangsgeschwindigkeit)
α (Winkel zur Erde)

Gesucht:

1. Flugzeit vom Körper. t_F

2.Höhe der Flugbahn h.

3.Flugbahnlänge L.

4.Beschreibung der Flugbahn mathematisch . Funktion y(x)

Schreiben wir die Formeln Komponentweise für x und y auf.

Die Formeln zusammengefasst und gekürzt.

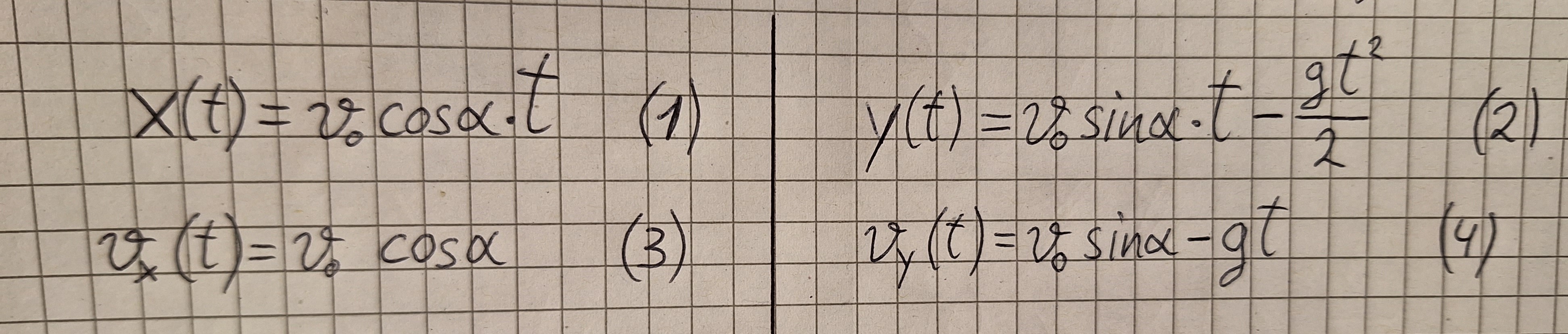
An der Linken Gleichung sieht man das der Körper in der x Richtung sich gleichmäßig bewegt. Es gibt keine Beschleunigung und die Geschwindigkeit v_x ist immer gleich.

In y Richtung ist die Bewegung gleichmäßig beschleunigt. Das sieht man an den rechten Gleichungen. g ist die Fallbeschleunigung.

Die Bewegung in y Richtung kann man sich vorstellen, als ob mann einen Körper senkrecht nach oben wirft und er dann wieder runterfällt.

An der Formel sieht man v_y(t) (Geschwindigkeit in y Richtung) wird mit der Zeit immer kleiner und am obersten Punkt wird v_y=0 danach wird v_y negativ und der Körper fällt runter.

Mann kann diese Bewegung in zwei Richtungen zerlegen, waagerechte und senkrechte (x und y). In waagerechter Richtung bewegt sich der Körper gleichmäßig mit gleicher Geschwindigkeit und in senkrechter Richtung bewegt sich der Körpler mit Beschleunigung.

Berechnung der gesuchten Werte.

1. Flugzeit t_f berechnen.

Das Ende der Flugzeit ist dann wenn der Körper auf die Erde fällt, also y=0 ist.

Aus Formel (2).

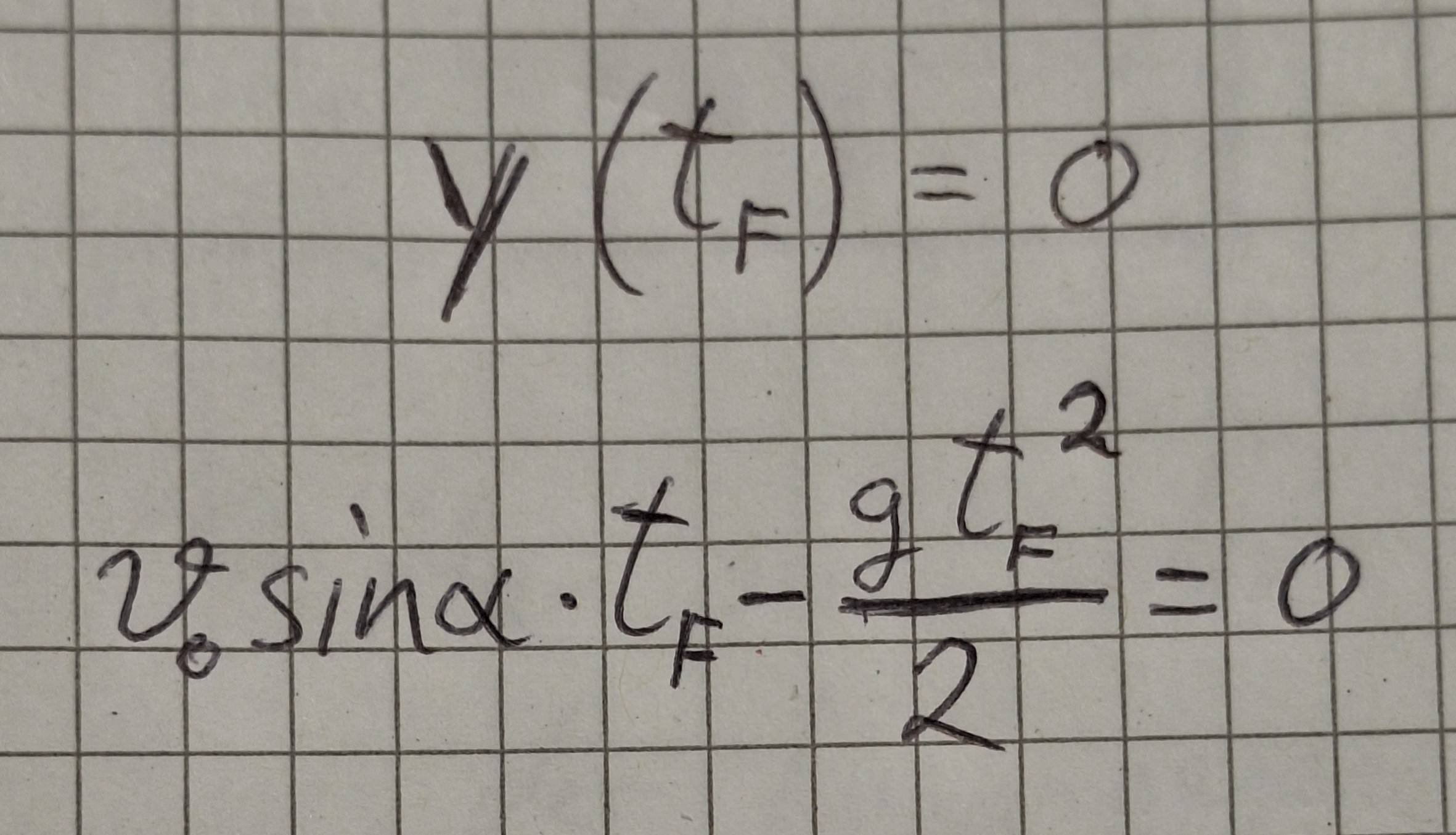
Das ist eine quadratische Gleichung , sie hat zwei Lösungen, eine ist Null. Das ist die Zeit in der der Körper geworfen wurde. Die Flugzeit ist größer Null.

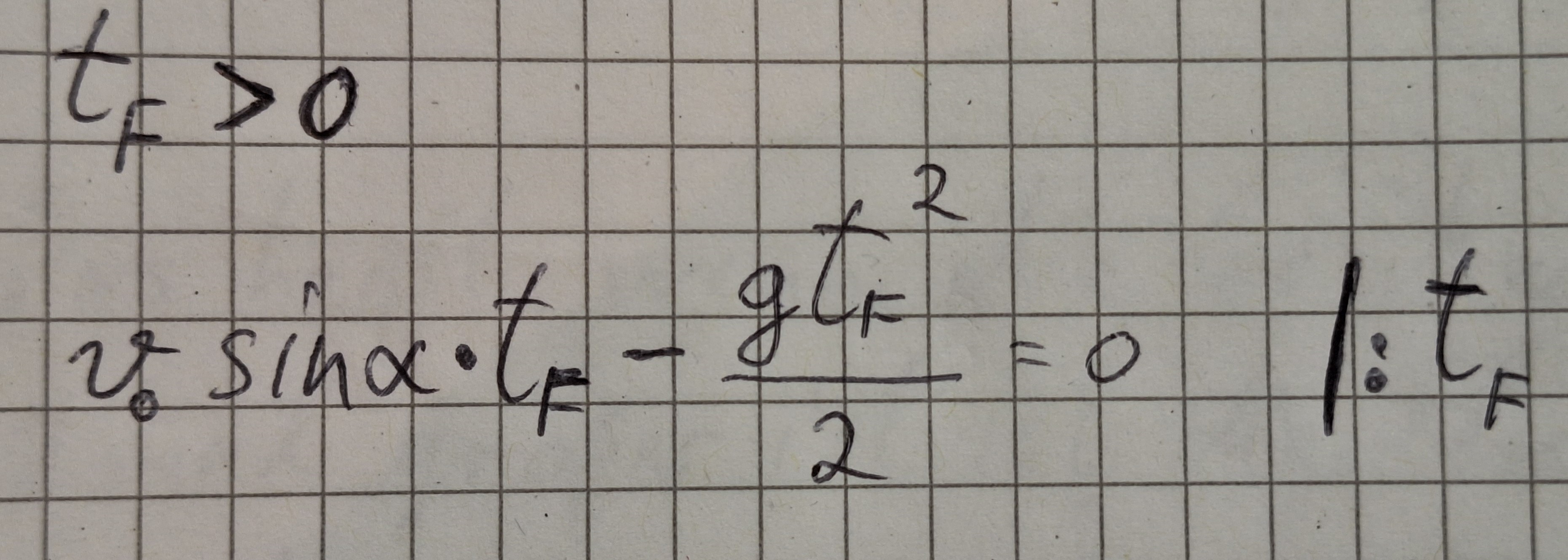
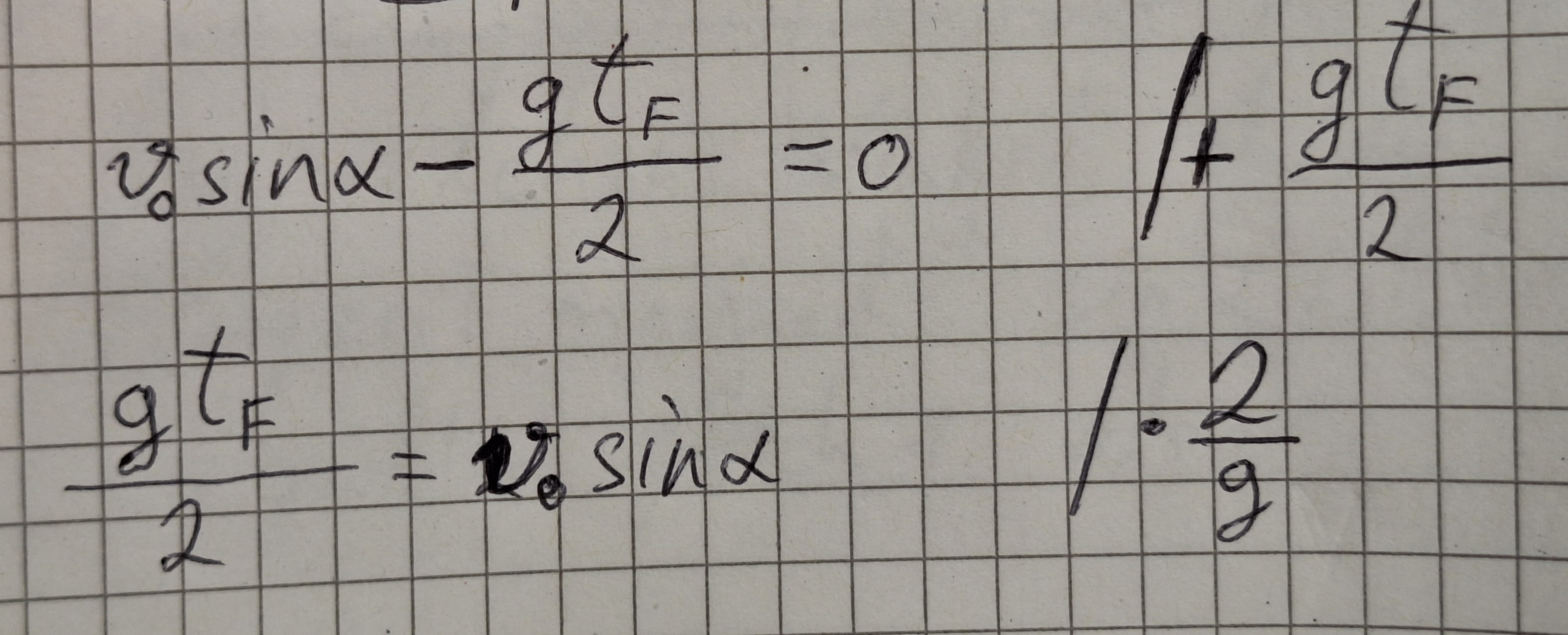
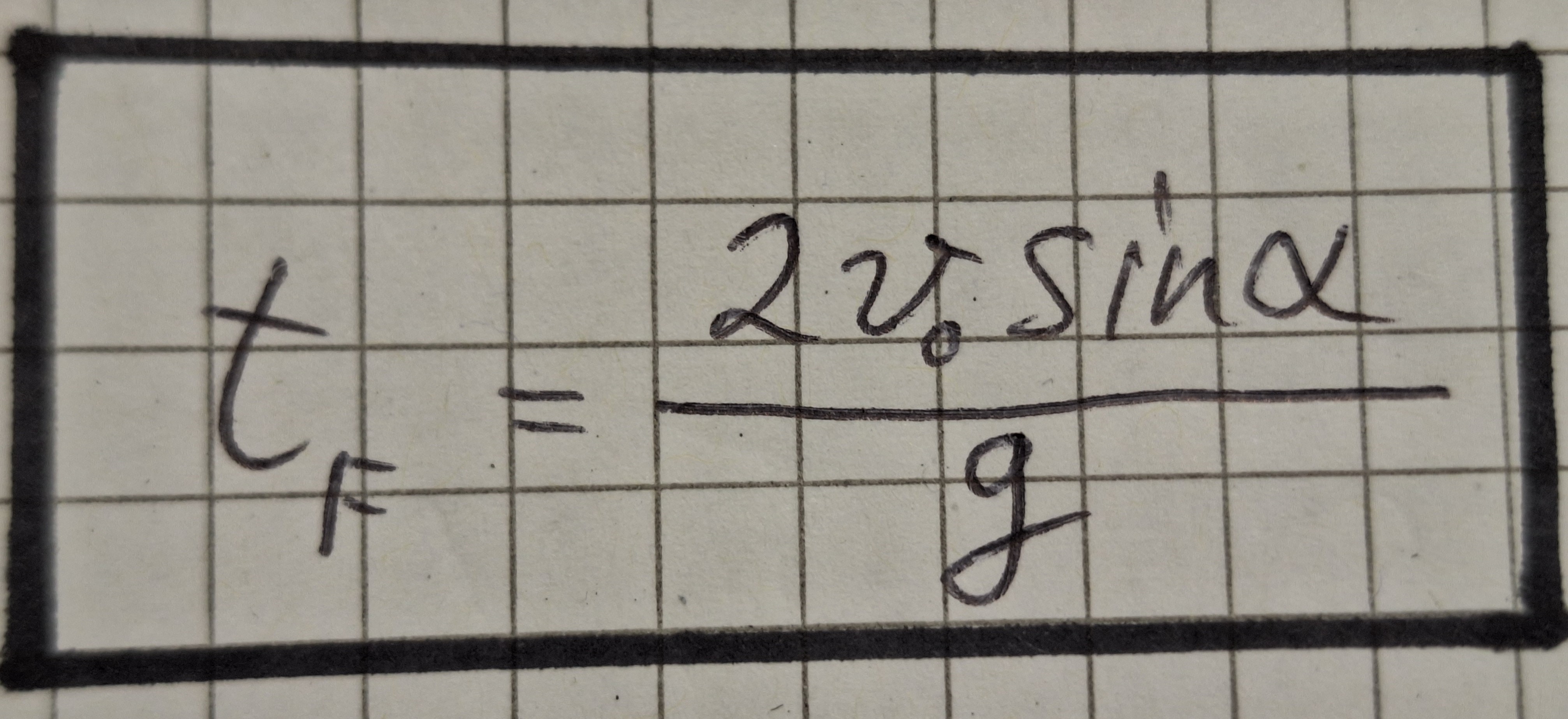
Man sieht die Flugzeit t_f hängt von der Anfangsgeschwindigkeit v₀ dem Winkel α, und der Beschleunigung g ab.

Eigenschaften der Formel.

1. 
   
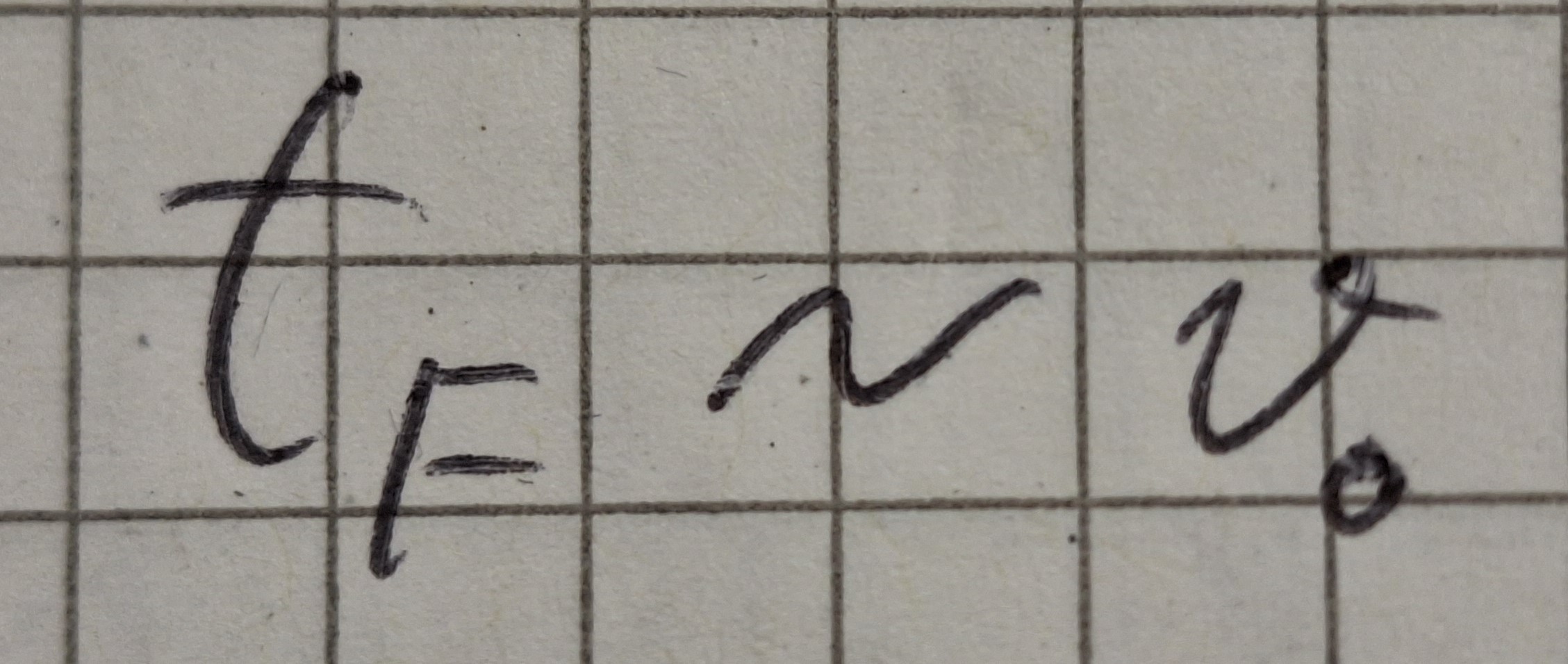
   Flugzeit ist Proportional zu Anfangsgeschwindigkeit.
   Das heißt wenn die Geschwindigkeit zweimal größer ist ist die Flugzeit zweimal größer.
2. 
   
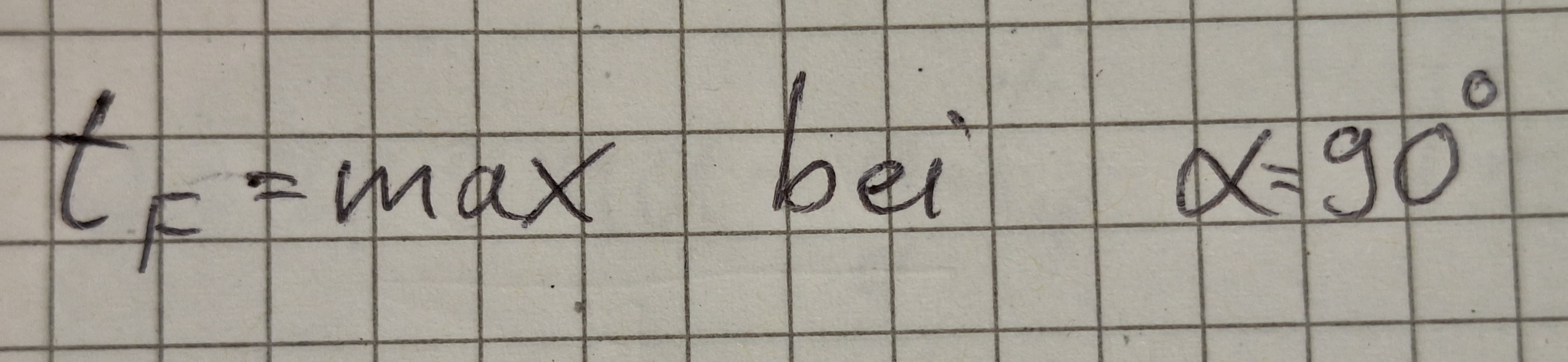
   Die Flugzeit ist maximal bei α=90° .
   sin α ist bei 90° gleich 1.
3. 
   
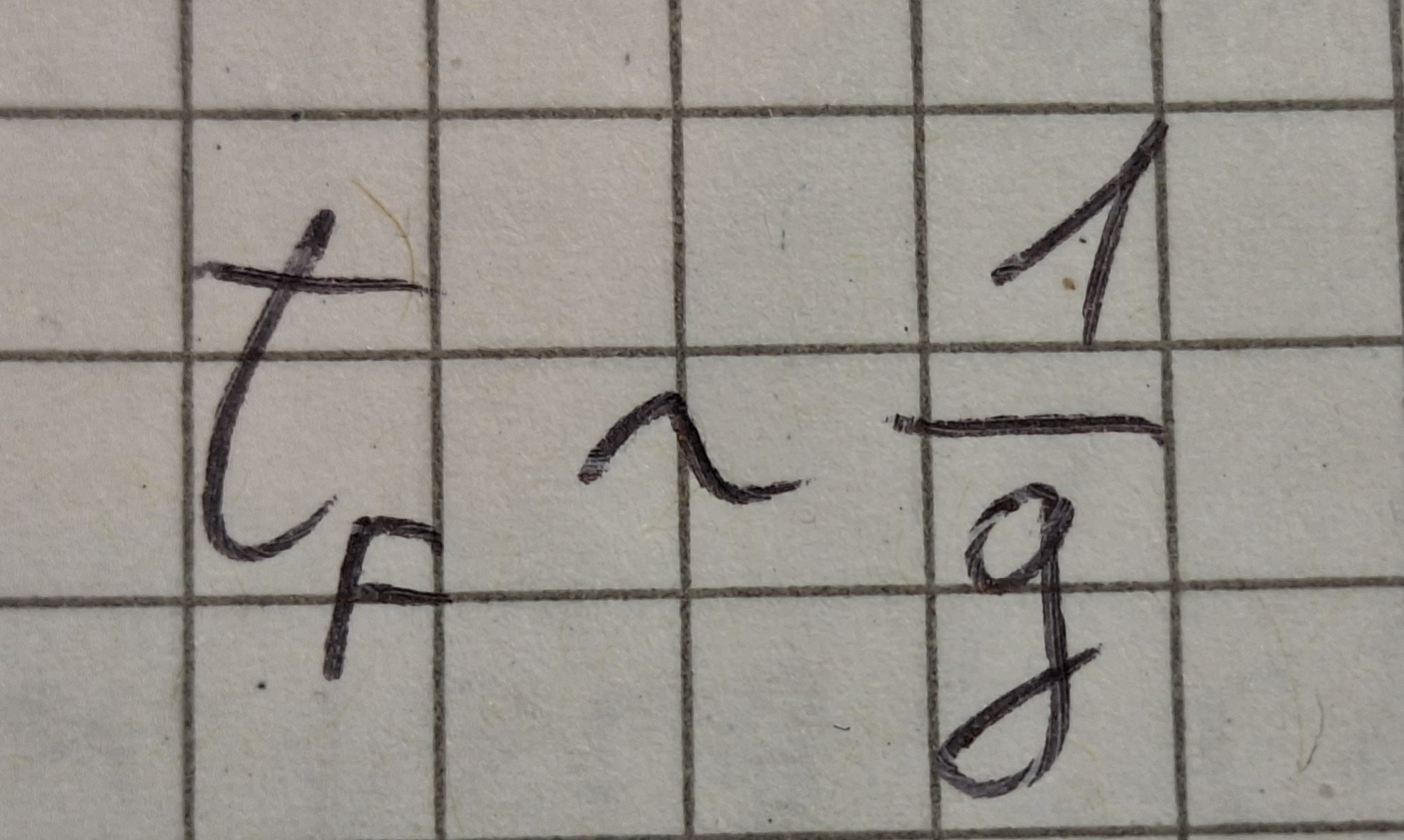
   Flugzeit ist antiproportional zu Beschleunigung. Bei 2 mal kleinerer Beschleunigung ist die Flugzeit 2 mal größer.

2. Die maximale Höhe h berechnen.

Am höchsten Punkt ist die Geschwindigkeit v_y gleich Null.

Wenn y=h ist v_y=0.

Aus Formel (4).

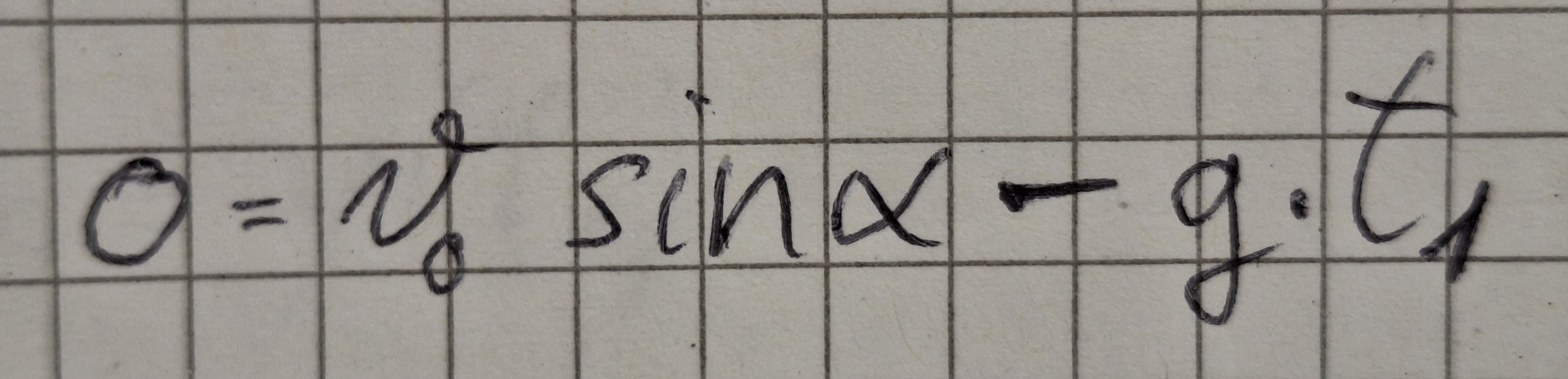
t₁ - ist die Zeit in der der Körper die maximale Höhe erreicht.

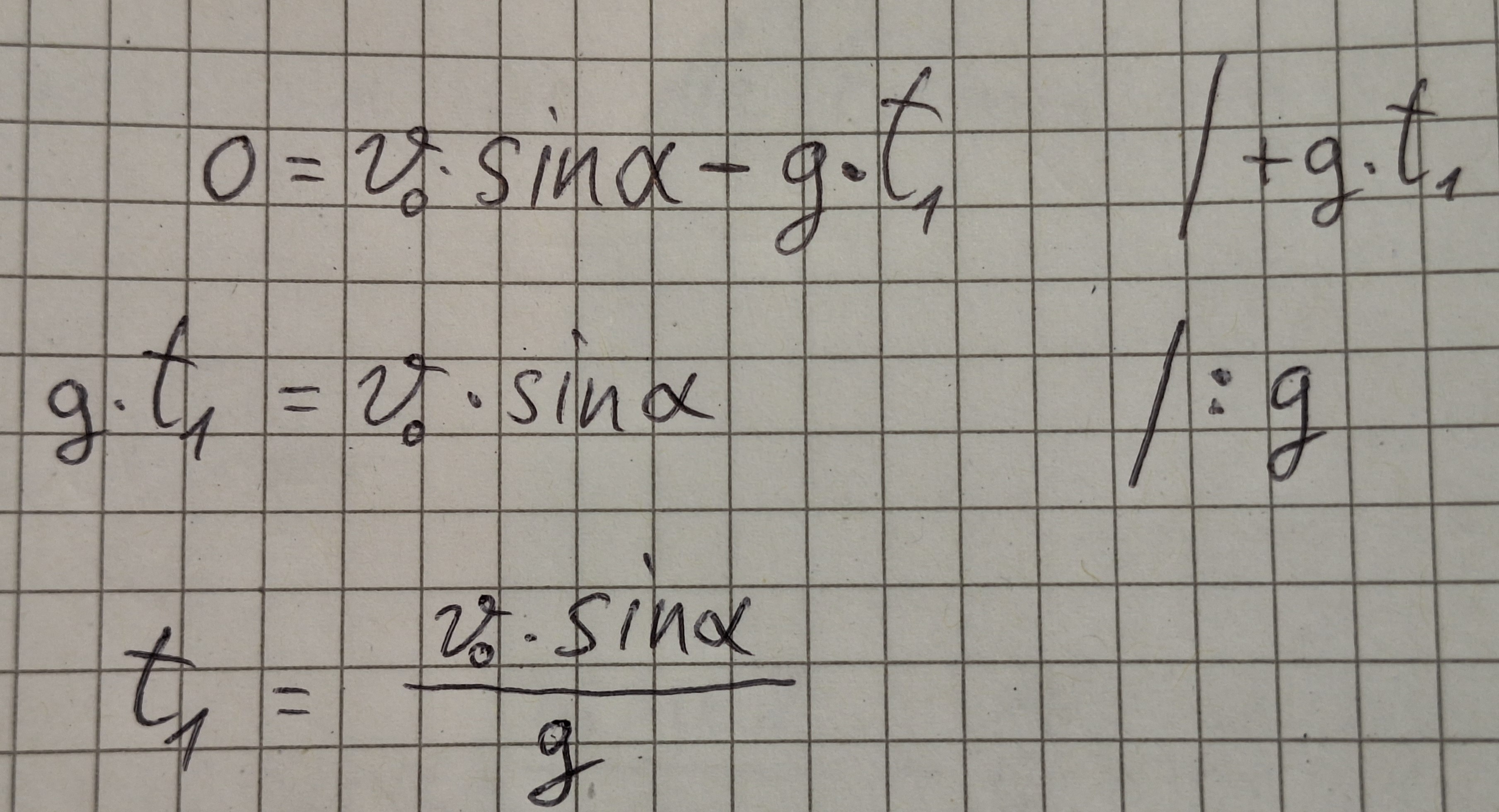
Im vergleich zu der Formel der Flugzeit , sieht man das t₁ halb so groß ist wie t_F (Flugzeit) ist.

Die hälfte der Flugzeit fliegt der Körper nach oben und die hälfte nach unten.

Um die maximale Höhe h zu berechnen, berechnen wir y im zeitpunkt t₁.
y(t₁)

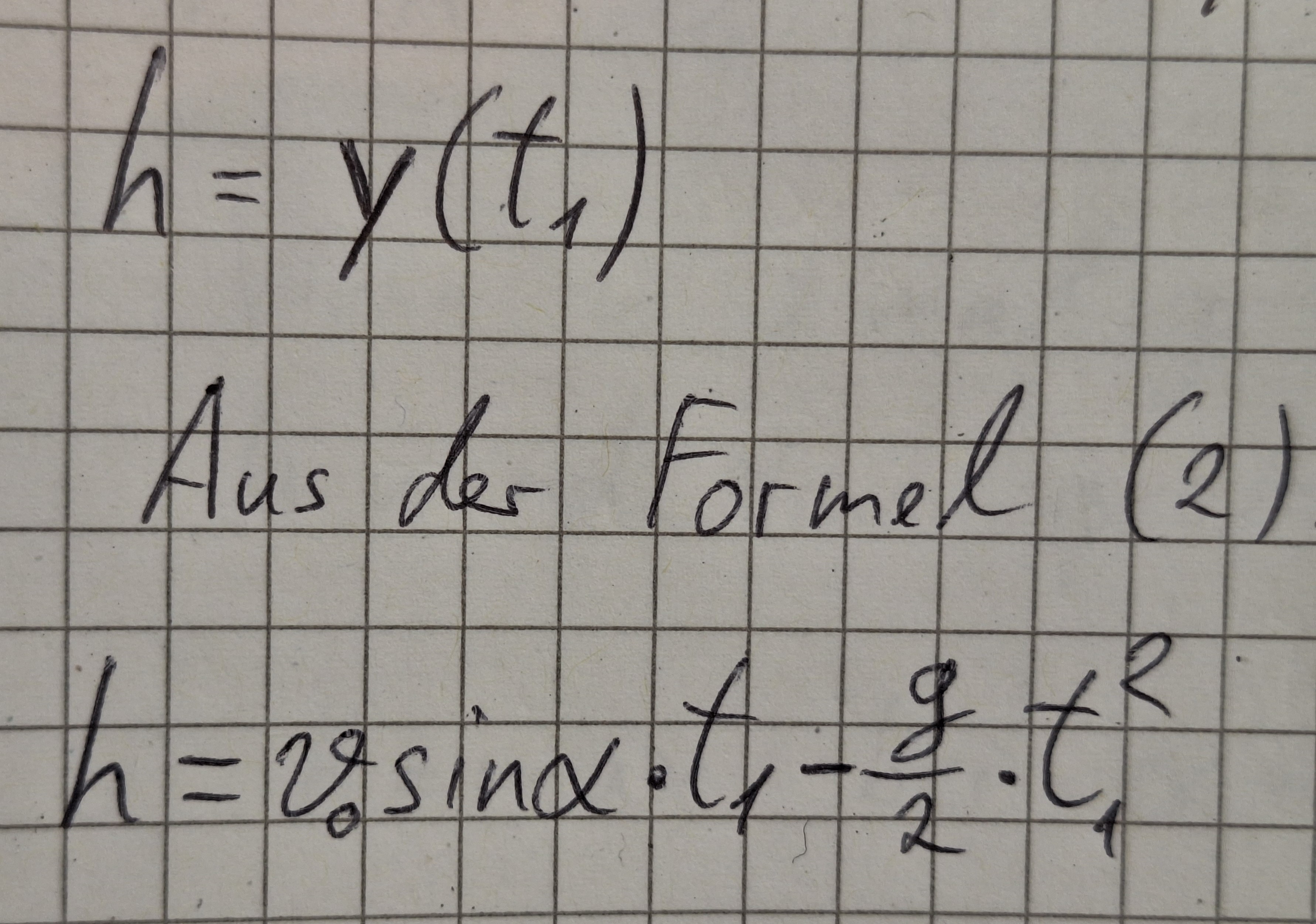
Dann setzen wir die Formel von t₁ ein.

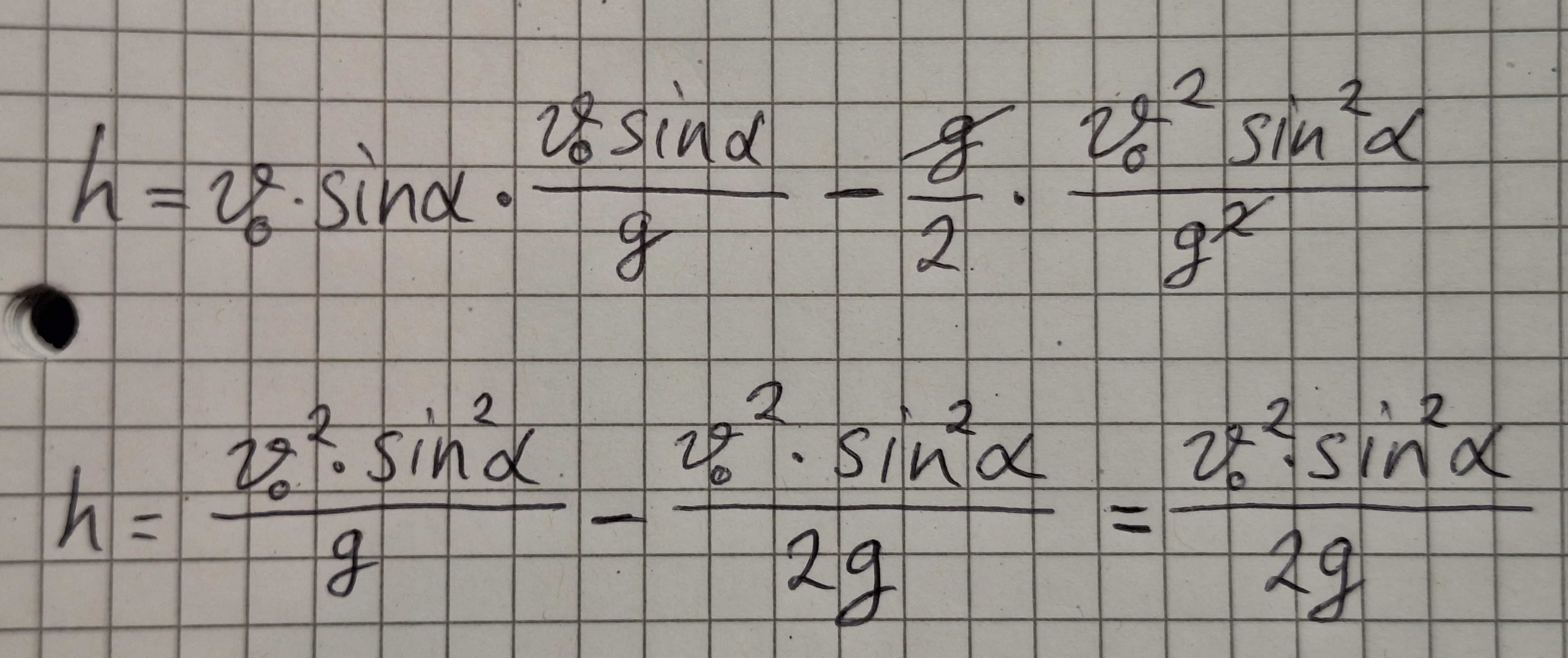
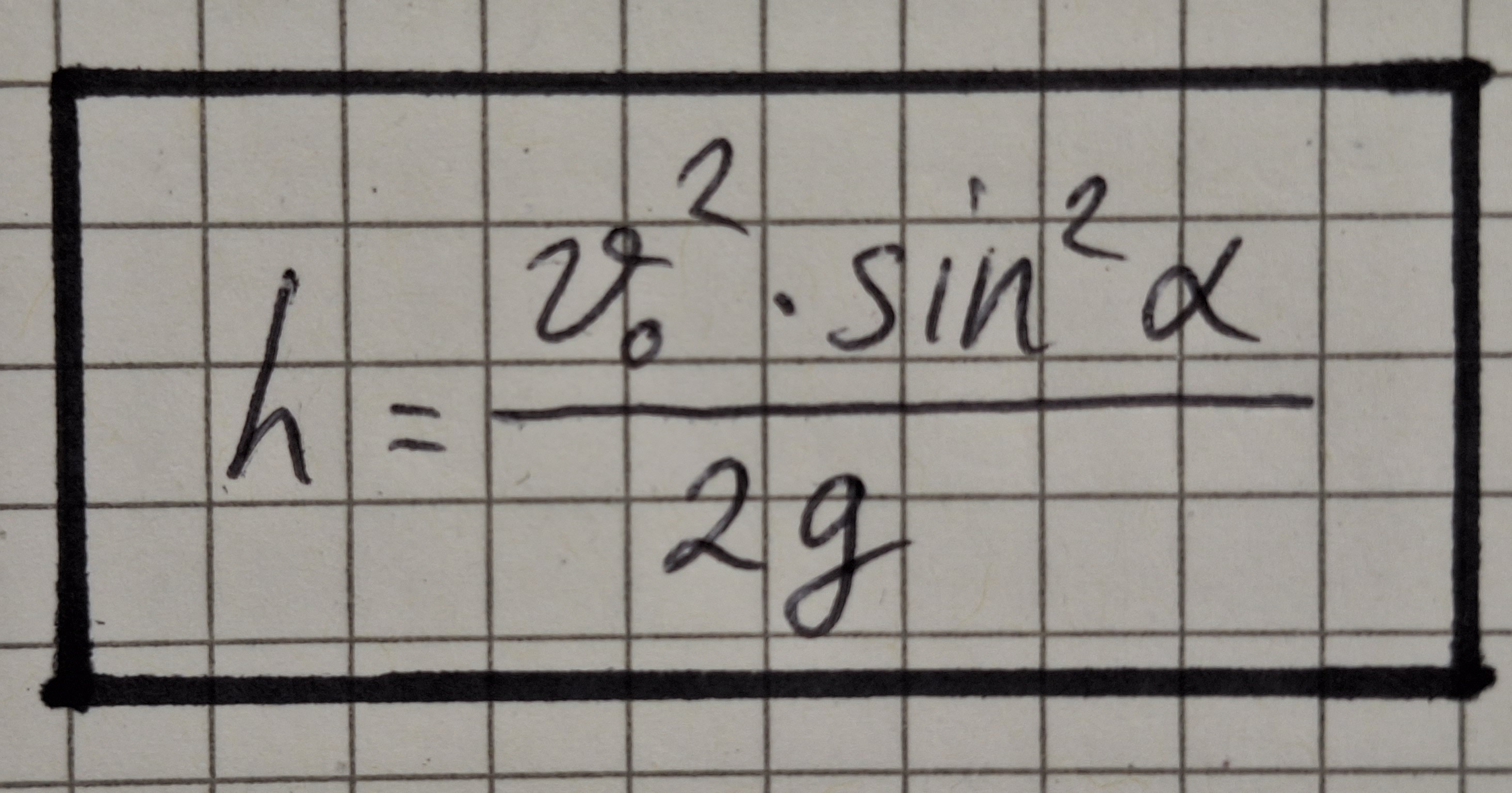
Eigenschaften der Formel.

1. 
   h~v₀²
   Wenn die Anfangsgeschwindigkeit v₀ 2 mal größer wird, dann wird h 4 mal größer.
2. 
   h=max bei α=90°
3. 
   h~1/g

3. Flugbahnlänge L berechnen.

L=x(t_F)

Flugbahnlänge L ist gleich x im Zeitpunkt der Flugzeit t_F

Aus Formel (1)

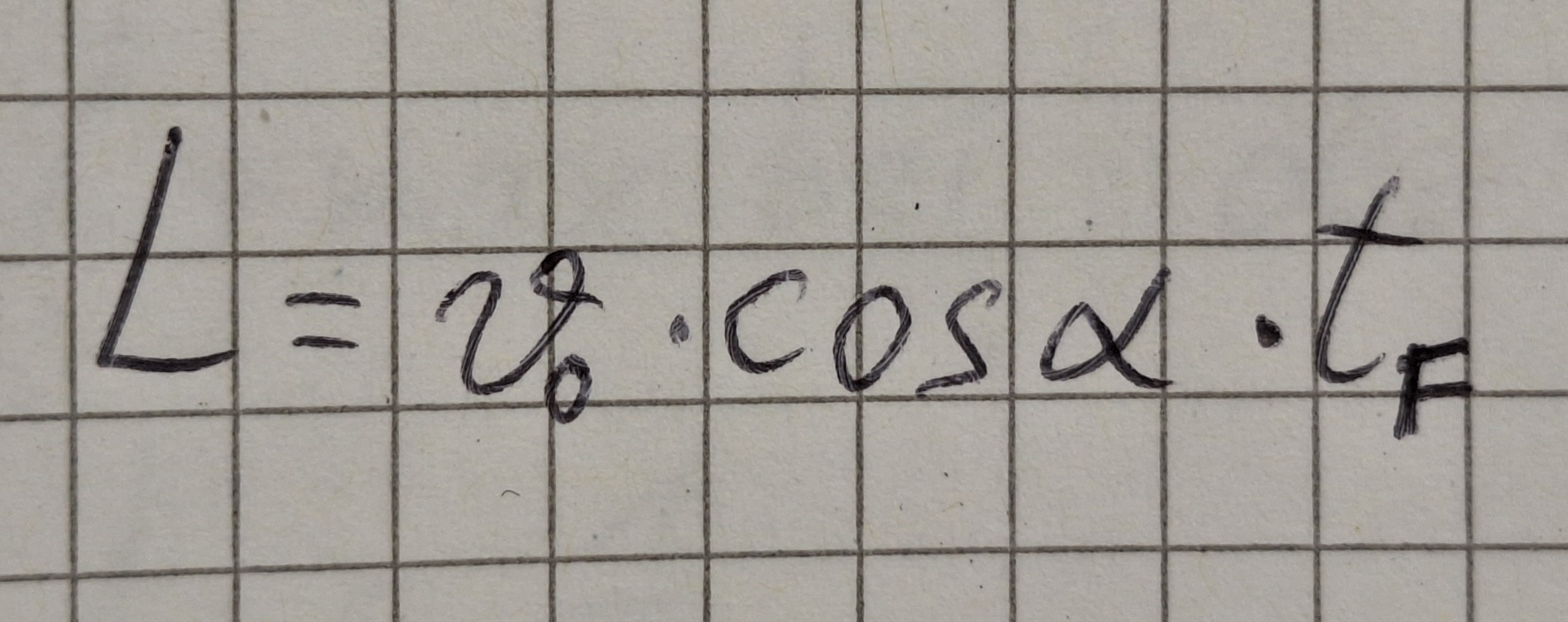
Formel von t_F einsetzen.

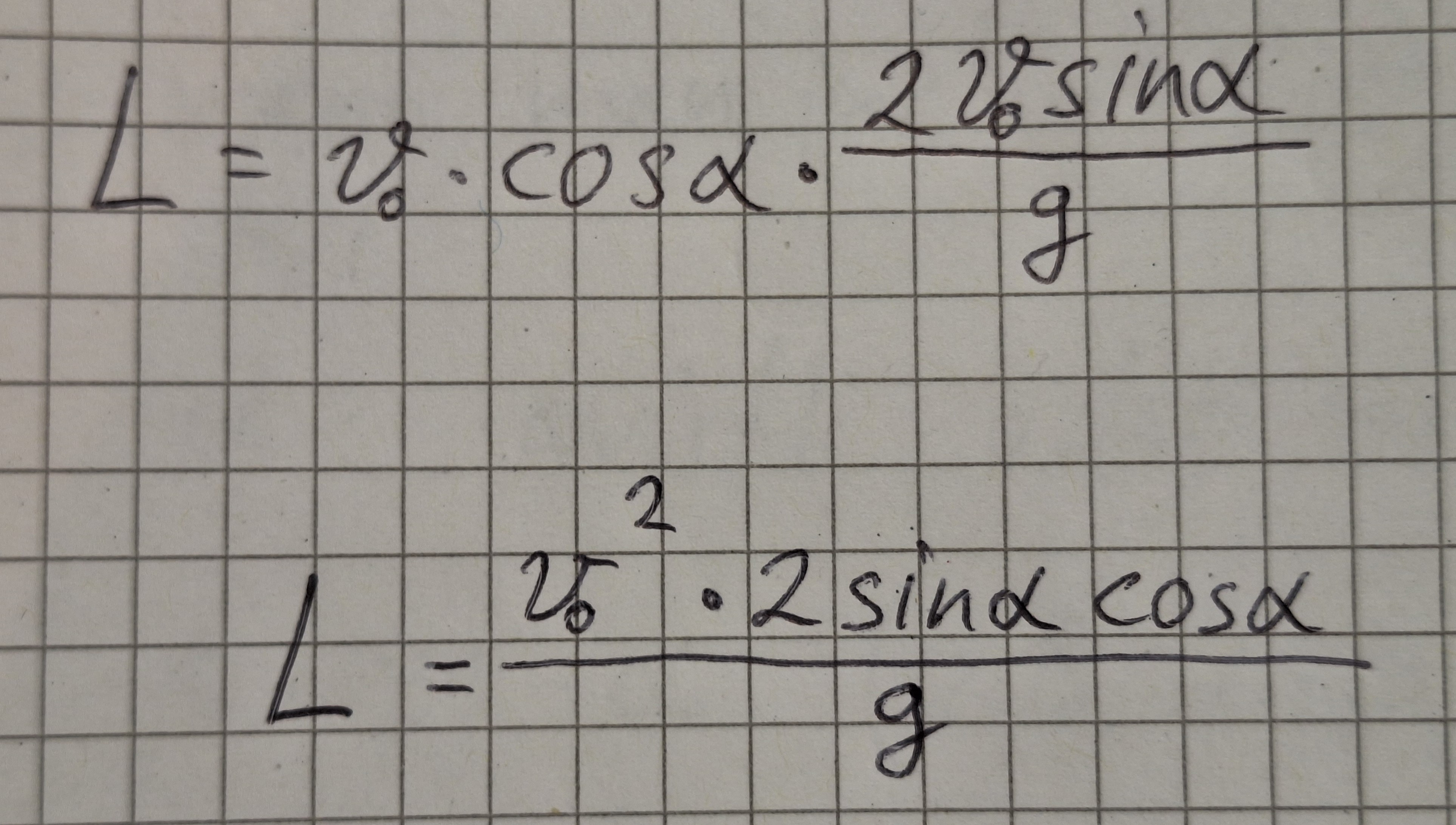
Mathematik Formel von Sinus und Cosinus.

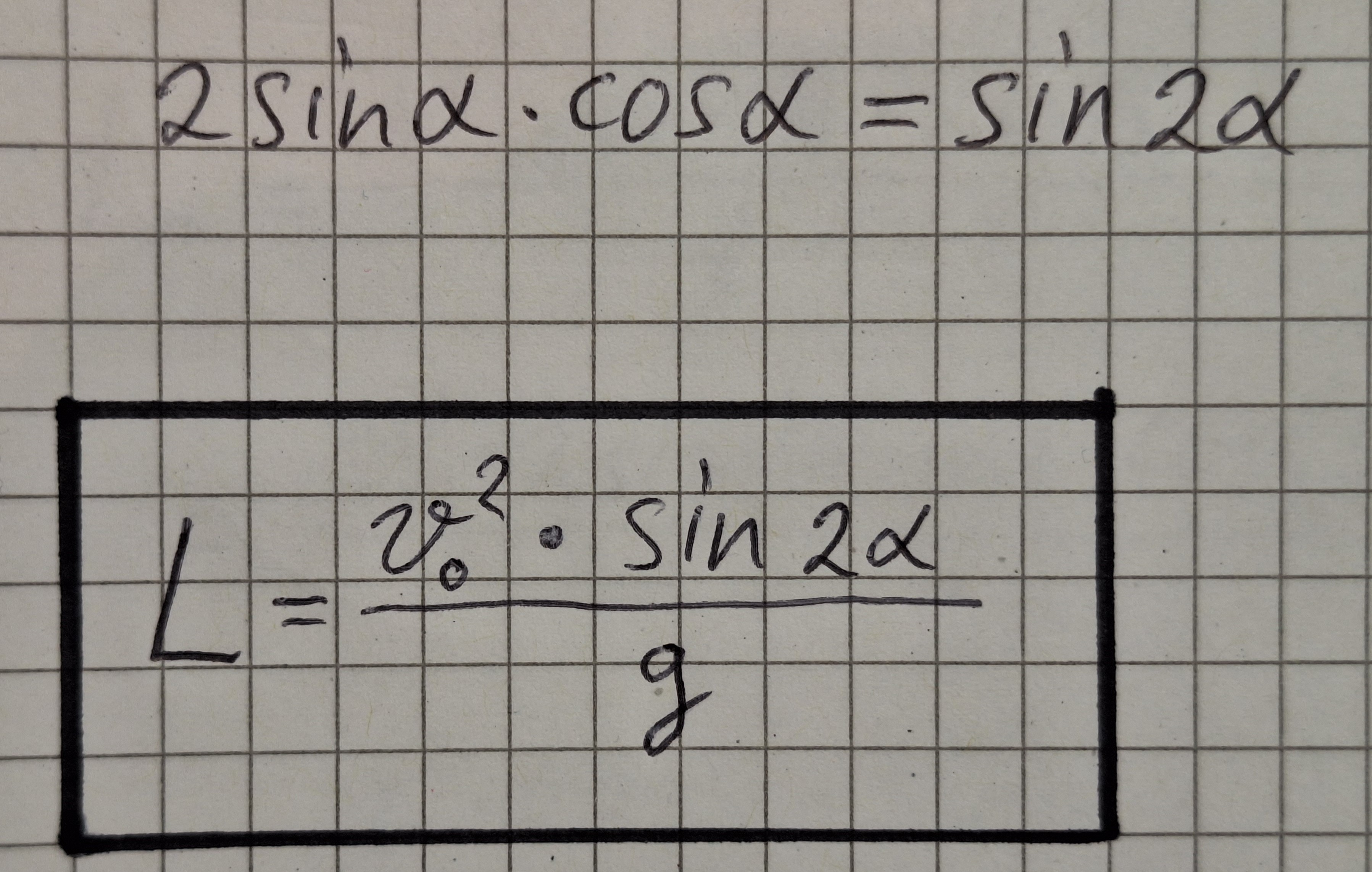
Eigenschaften der Formel.

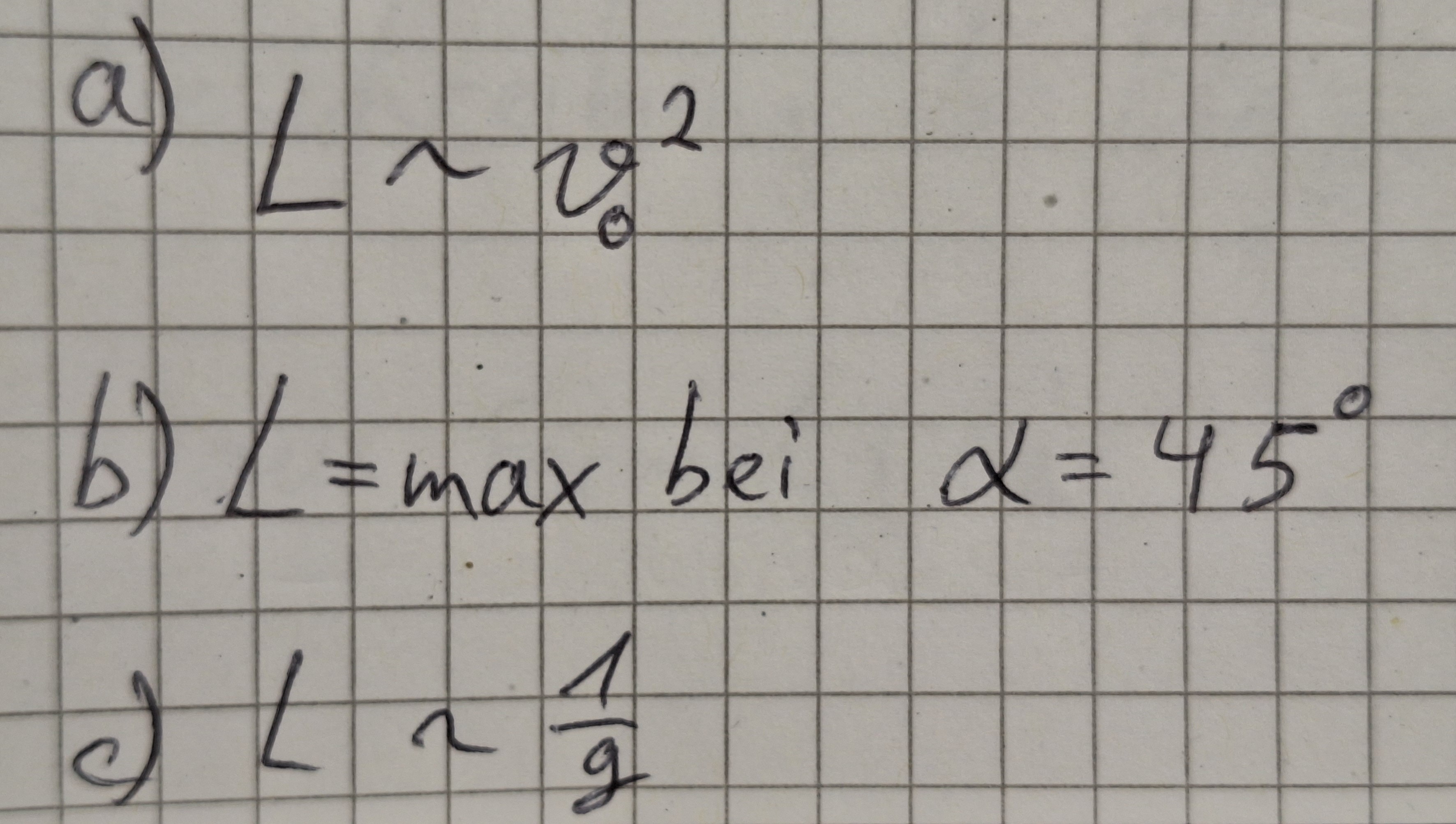
An der Formel sieht man das wenn man mit dem Winkel α wirft oder mit dem Winkel β = 90°-α (z.B. α=30° und β = 90°-30°=60°) dann ist Flugbahnlänge L gleich groß.

Beweis.

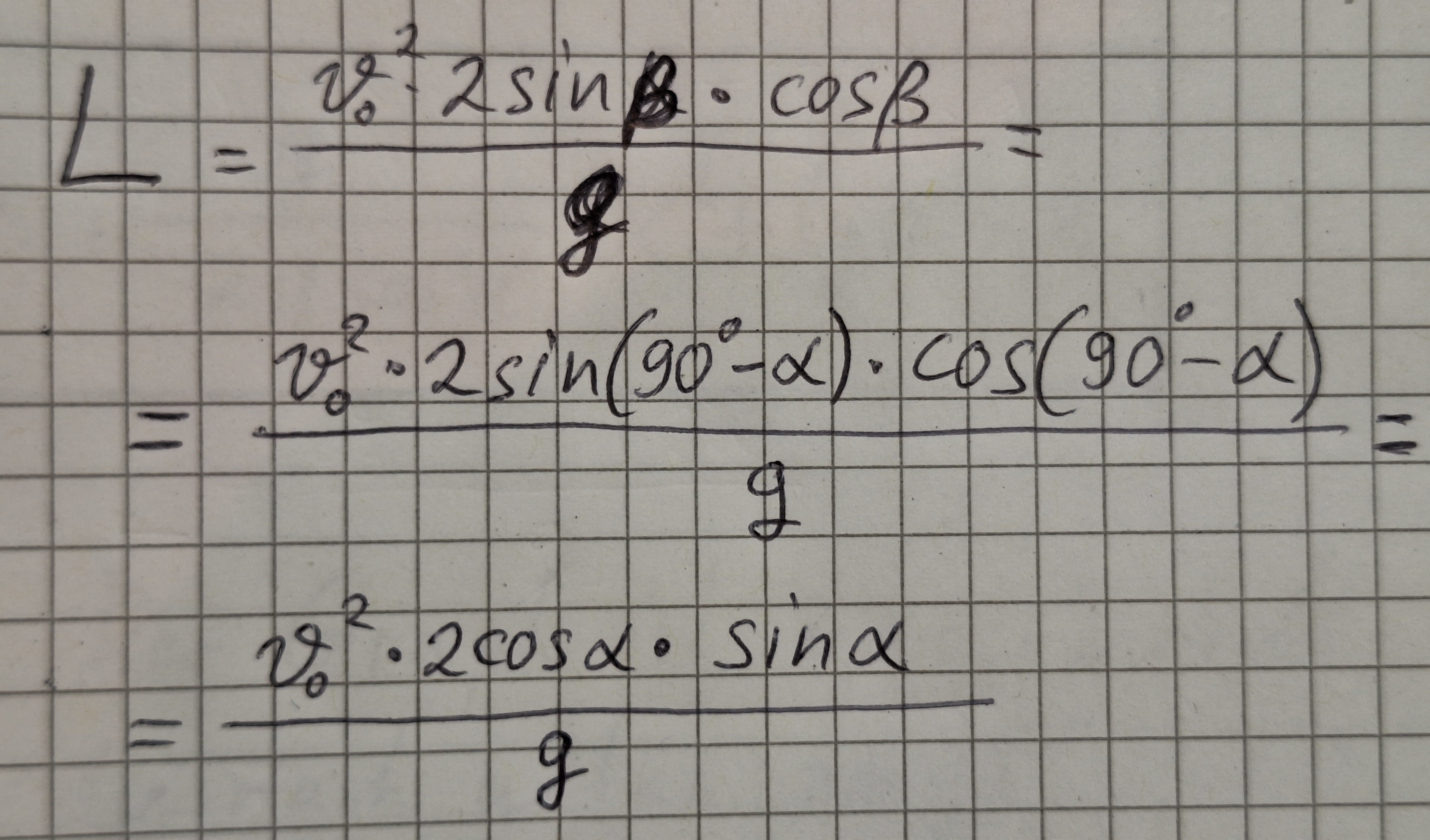
3. Beschreibung der Flugbahn mathematisch. y(x).

Aus Formel (1).

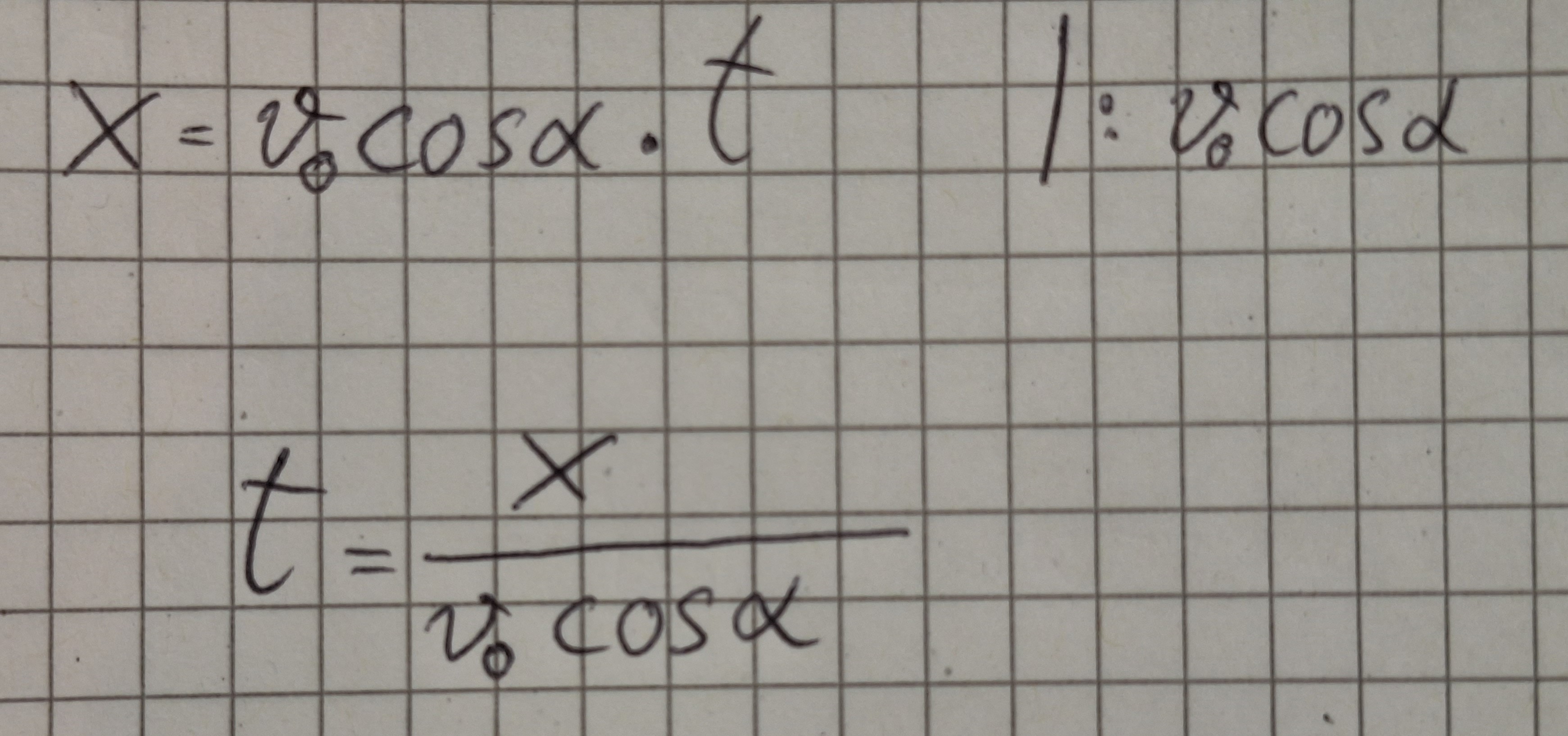
Einsetzen in Formel (2).

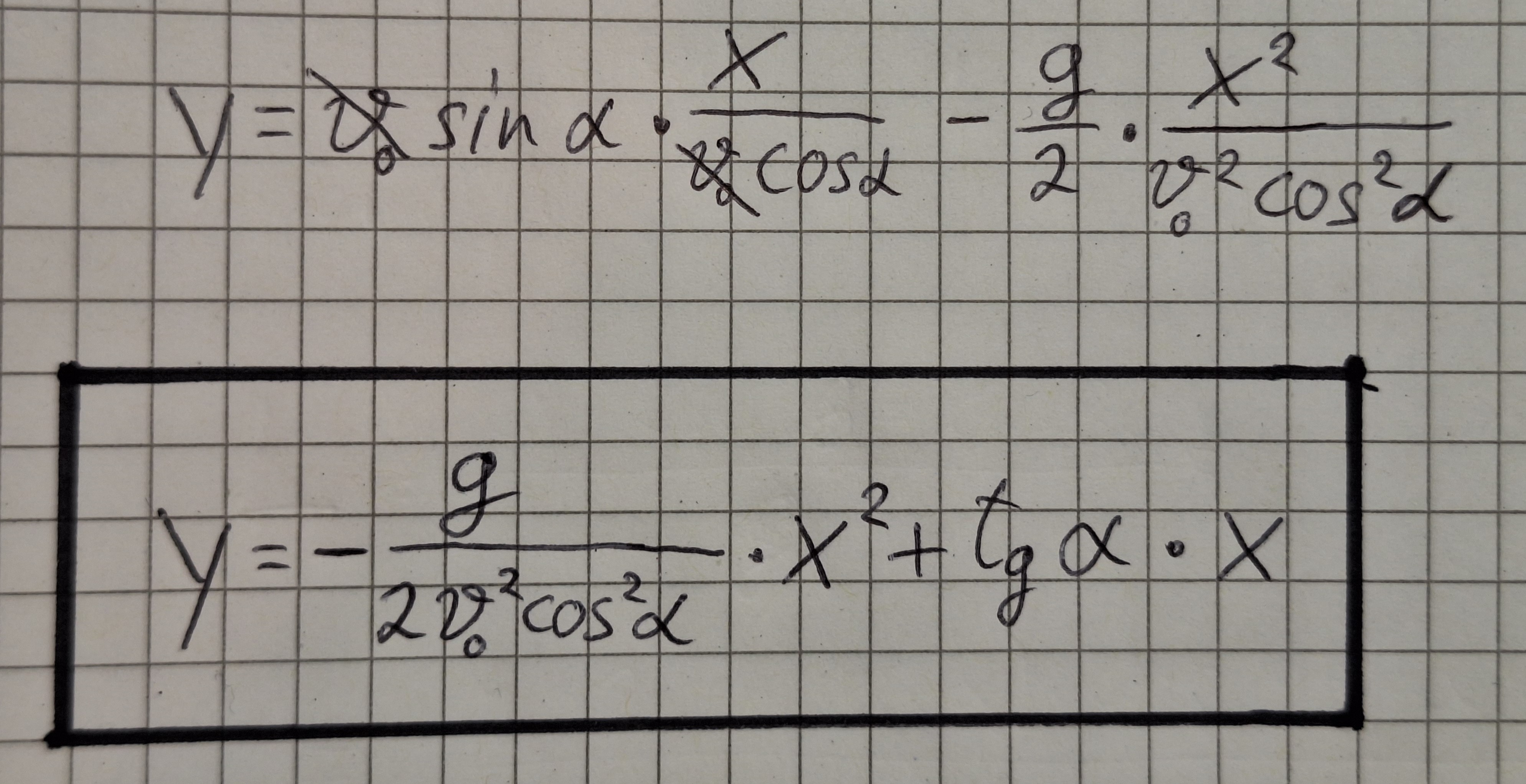
Der Graph der Funktion ist eine Parabel die nach unten zeigt.