Gleichmäßig beschleunigte Bewegung. Beschleunigung.Graphische Beschreibung.

Ein Diagramm: Geschwindigkeits Projektion auf die Achse x in Abhängigkeit von der Zeit .

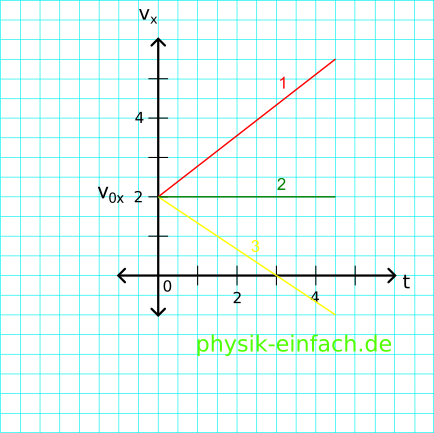
v_0x - Anfangsgeschwindigkeit (Projektion auf Achse x).

a_x - Beschleunigung (Projektion auf Achse x).

t - Zeit

Die Anfangsgeschwindigkeit ist bei allen gleich:
v_0x= 2m/s

Um die Beschleunigung zu Berechnen brauchen wir die Formel:

\[a_{x}=\frac{v_{x}-v_{0x}}{t}\]

Für die Funktionsgleichung die Formel:

\[v_{x}(t)=v_{0x}+a_{x} t\]

Funktion Nr.1:

\[a_{x}=\frac{5,5-2}{4,5}=0,78\frac{m}{s^{2}}\]

\[v_{x}(t)=2+0,78t\]

Funktion Nr.2:

\[a_{x}=0\]

\[v_{x}(t)=2\]

Funktion Nr.3:

\[a_{x}=\frac{-1-2}{4,5}=-0,67m/s^{2}\]

\[v_{x}(t)=2-0,67t\]

Berechnung von der zurückgelegten Strecke.

Ein v_x(t) Diagramm: \(v_{x}(t)=v_{0x}+a_{x} t\)

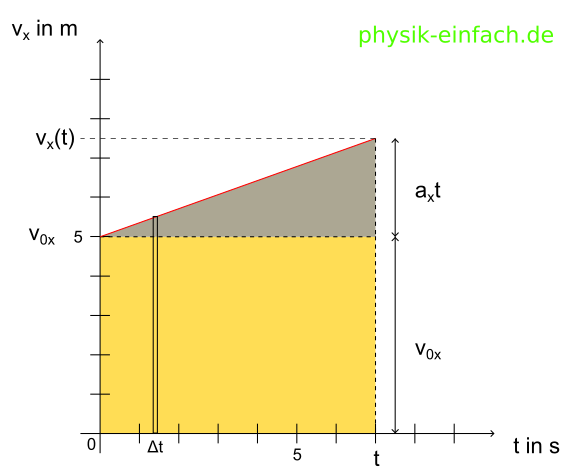
v_0x - Anfangsgeschwindigkeit (Projektion auf Achse x).

a_x - Beschleunigung (Projektion auf Achse x).

t - Zeit

S_x - Sterecke (Projektion auf Achse x).

Die Fläche unter dem Graphen ist die Zurückgelegte Strecke.

Erklärung.

Wenn wir einen sehr kleinen Zeitintervall delta t nehmen dann kann man sagen, das die Geschwindigkeit in dem Zeitintervall gleich ist (sich nicht ändert). Und Geschwindigleit multipliziert mit Zeit ist die zurückgelegte Strecke und auch die Fläche unter dem Graphintervall. Wenn wir viele solche Zeitintervale zusammenlegen ist es die Fläche unter dem Graph.

Wir berechnen die Fläche unter dem Graph , das ist dann die zurückgelegte Strecke.

Die Fläche von Rechteck berechnet man mit der Formel:

\[A=v_{0x}\cdot t\]

Die Fläche von Dreieck berechnet man mit der Formel:

\[A=\frac{a_{x}\cdot t^{2}}{2}\]

Also berechnet man die zurückgelegte Strecke. Mit der Formel:

\[S_{x}=v_{0x}\cdot t +\frac{a_{x}\cdot t^{2}}{2}\]

Vektorielle Formel.

\[\vec{S}=\vec{v}_{0}\cdot t +\frac{\vec{a}\cdot t^{2}}{2}\]