Zum Umrechner.

Streckenberechnung ohne t (Zeit).

Durchschnittliche Geschwindigkeit bei gleichmäßiger geradliniger Beschleunigung.

Für die Herleitung der durchschnittlichen Geschwindigkeit brauchen wir diese bekannten Formeln.

(1)\[\vec{v}_{durch}=\frac{\vec{S}}{t}\]

(2)\[\vec{S}=\vec{v}_{0}t+\frac{\vec{a}t^{2}}{2}\]

(3)\[\vec{v}=\vec{v}_{0}+\vec{a}t\]

\[\vec{a}t=\vec{v}-\vec{v}_{0}\]

Formel (2) in Formel (1) eisetzen

\[\vec{v}_{durch}=\frac{\vec{v}_{0}t+\frac{\vec{a}t^{2}}{2}}{t}= \vec{v}_{0}+\frac{\vec{a}t}{2}\]

Statt at Formel 3 einsetzen.

\[\vec{v}_{durch}=\vec{v}_{0}+\frac{\vec{v}-\vec{v}_{0}}{2}=\vec{v}_{0}+\frac{\vec{v}}{2}-\frac{\vec{v}_{0}}{2}=\frac{\vec{v}}{2}+\frac{\vec{v}_{0}}{2}=\frac{\vec{v}+\vec{v}_{0}}{2}\]

Wichtige Formeln.

Komponentweise Projektion auf die x Achse

Das Wichtige ist, man braucht nur die Anfangsgeschwindigkeit und Endgeschwindigkeit zu kennen, ohne die Beschleunigung.

Das ist Nützlich z.B. bei einer Aufgabe bei der die Beschleunigung nicht gegeben ist.

Ein Diagramm von v_x(t).

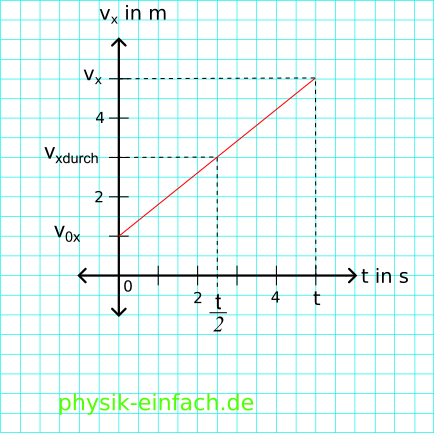
Wichtig:

In der halben Zeit ist die Geschwindigkeit gleich der Durchschnittlichen Geschwindigkeit. In der halben Strecke ist es aber nicht so. Das sieht man gut im Funktionsgraph. Die Strecke ist ja die Fläche unter dem Graph.

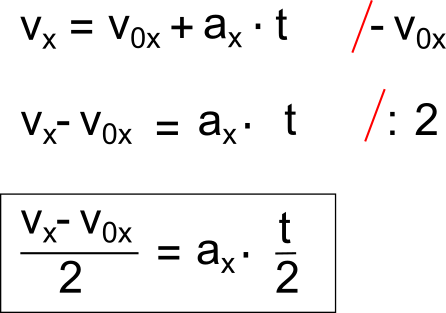
Der Mathematische Beweis dazu.

Noch eine Formel, mit der mann die Strecke berechnet, wenn Anfangsgeschwindigkeit, Endgeschwindigkeit und Beschleunigung gegeben sind.

Herleitung der komponentweise Formel für die berechnung der Strecke , mit bekanter Anfangsgeschwindigkeit , Endgeschwindigkeit und Beschleunigung .

(1)\[v_{x}=v_{0x}+a_{x}t \]

(2)\[a_{x}t=v_{x}-v_{0x}\]

(3)\[t=\frac{v_{x}-v_{0x}}{a_{x}}\]

Setzen wir Formel 3 in diese bekannte Formel ein.

\[S_{x}= \frac{v_{x}+v_{0x}}{2}\cdot t\]

\[S_{x}= \frac{v_{x}+v_{0x}}{2}\cdot \frac{v_{x}-v_{0x}}{a_{x}}\]

\[S_{x}= \frac{v_{x}^{2}-v_{0x}^{2}}{2a_{x}}\]